Question

【题目】若函数(M＞0，＞0，0＜＜)的最小值是﹣2，最小正周期是2，且图象经过点N(，1).

（1）求的解析式；

（2）在△ABC中，若，，求cosC的值.

Answer 1

【答案】（1）.（2）

【解析】

（1）利用三角函数的性质：最值求出M，最小正周期求出，特殊点代入求出，即可求出解析式.

（2）首先利用解析式求出，，再利用同角三角函数的基本关系求出、，然后结合三角形的内角和性质以及两角和的余弦公式即可求解.

解：（1）因为的最小值是﹣2，所以M＝2.

因为的最小正周期是2，即，所以＝1，

又由的图象经过点(，1)，可得，，

所以或，kZ，

又0＜＜，所以，故，即.

（2）由（1）知，又，，

故，，即，，

又因为△ABC中，A，B(0，)，

所以，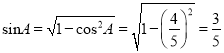

，

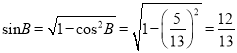所以cosC＝cos[﹣(A＋B)]＝﹣cos(A＋B)＝﹣(cosAcosB﹣sinAsinB)

＝.