Question

【题目】如图，公园里有一湖泊，其边界由两条线段和以为直径的半圆弧组成，其中为2百米，为．若在半圆弧，线段，线段上各建一个观赏亭，再修两条栈道，使. 记．

（1）试用表示的长；

（2）试确定点的位置，使两条栈道长度之和最大.

Answer 1

【答案】（1）；（2）与重合.

【解析】分析：（1）解直角三角形BDC用表示的长.(2)先利用正弦定理求出DF＝4cosθsin(＋θ)， 再求出DE＝AF=4－4，再利用三角函数求DE＋DF的最大值.

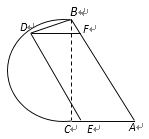
详解：（1）连结DC．

在△ABC中，AC为2百米，AC⊥BC，∠A为，

所以∠CBA＝，AB＝4，BC＝．

因为BC为直径，所以∠BDC＝，

所以BD＝BC cosθ＝cosθ．

（2）在△BDF中，∠DBF＝θ＋，∠BFD＝，BD＝cosθ，

所以，

所以DF＝4cosθsin(＋θ)，

且BF＝4，所以DE＝AF=4－4，

所以DE＋DF＝4－4＋4 sin(＋θ)= sin2θ－cos2θ＋3

＝2 sin(2θ－)＋3．

因为≤θ＜，所以≤2θ－＜，

所以当2θ－＝，即θ＝时，DE＋DF有最大值5，此时E与C重合．

答：当E与C重合时，两条栈道长度之和最大．