题目内容
（本题满分15分）
已知函数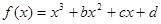
的图象过点P
,
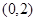且在点M
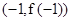处的切线方程为
.
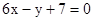(1) 求函数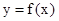
的解析式; (2) 求函数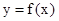的单调区间.
【答案】
(1) 
(2) 
的增区间是
和
,
减区间是
【解析】解: (1) 由
的图象经过P
,知
, …………………………2分
所以
.即
由在
处的切线方程是
, 知
,
……5分
故所求的解析式是 ……7分
(2) 
令
即
解得 
……10分
当
当
……14分
故的增区间是和,
减区间是.……15分
思路分析：第一问中，由的图象经过P,知,所以
.即
由在处的切线方程是, 知
得到b,c的值。
第二问中。令即
解得
当
当得到结论。
练习册系列答案
阅读快车系列答案
相关题目
．
在
上单调递增，在
上单调递减，求实数
的最大值；
对任意的
，
都成立，求实数
的取值范围．
为自然对数的底数．
与曲线
相切
在
上恰有两个不等的实数根
，求
的大小
：
（
），焦点为
，直线
交抛物线
、
两点，
是线段
的中点，
轴的垂线交抛物线
，
到焦点
，求此时
的值；
是以
的单调区间；
，若
在
上不单调且仅在
处取得最大值，求
的取值范围．