题目内容
3.设数列{an}的各项都为正数,其前n项和为Sn.已知对任意n∈N,Sn是an2和an的等差中项.
(I)求数列{an}的通项公式an;
(Ⅱ)令cn=$\frac{1}{{a}_{n+1}^{2}-1}$,求{cn}的前n项和Wn.
分析 (I)由Sn是an2和an的等差中项.可得Sn=$\frac{{a}_{n}^{2}+{a}_{n}}{2}$,利用递推关系、等差数列的通项公式即可得出.
(II)cn=$\frac{1}{{a}_{n+1}^{2}-1}$=$\frac{1}{(n+1)^{2}-1}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用“裂项求和”即可得出.
解答 解:(I)∵Sn是an2和an的等差中项.
∴Sn=$\frac{{a}_{n}^{2}+{a}_{n}}{2}$,
∴当n=1时,a1=$\frac{{a}_{1}^{2}+{a}_{1}}{2}$,a1>0,解得a1=1.
当n≥2时,an=Sn-Sn-1=$\frac{{a}_{n}^{2}+{a}_{n}}{2}$-$\frac{{a}_{n-1}^{2}+{a}_{n-1}}{2}$,
化为:(an+an-1)(an-an-1-1)=0,
∵an>0,
∴an-an-1=1,
∴数列{an}是等差数列,公差为1,首项为1.
∴an=1+(n-1)=n.
(II)cn=$\frac{1}{{a}_{n+1}^{2}-1}$=$\frac{1}{(n+1)^{2}-1}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴{cn}的前n项和Wn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{n-1}-\frac{1}{n+1})$+$(\frac{1}{n}-\frac{1}{n+2})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$
=$\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$.
点评 本题考查了等差数列的通项公式及其递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

| A. | y=|x| | B. | y=3-x | C. | y=$\frac{1}{{x}^{3}}$ | D. | y=-x2+14 |
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
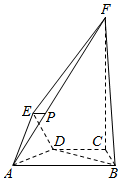 如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.
如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.