题目内容
2.已知$a={5^{-\frac{1}{2}}}$,b=ln2,c=log32,则( )| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | b>a>c |
分析 由于$a={5^{-\frac{1}{2}}}$=$\frac{1}{\sqrt{5}}$<$\frac{1}{2}$,b=ln2>$ln\root{3}{{e}^{2}}$=$\frac{2}{3}$,$\frac{1}{2}$<c=log32<$lo{g}_{3}\root{3}{{3}^{2}}$=$\frac{2}{3}$,即可得出大小关系.
解答 解:$a={5^{-\frac{1}{2}}}$=$\frac{1}{\sqrt{5}}$<$\frac{1}{2}$,
b=ln2=$ln\root{3}{8}$>$ln\root{3}{{e}^{2}}$=$\frac{2}{3}$,
$\frac{1}{2}$=$lo{g}_{3}\sqrt{3}$<c=log32=$lo{g}_{3}\root{3}{8}$<$lo{g}_{3}\root{3}{{3}^{2}}$=$\frac{2}{3}$,
∴b>c>a.
故选:B.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
7.对于函数f(x)=$\frac{x-1}{x+1}$,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*,且n≥2),令集合M={x|f2015(x)=-x,x∈R},则集合M为( )
| A. | 空集 | B. | 实数集 | C. | 单元素集 | D. | 二元素集 |
14.在等差数列{an}中,若3(a4+a6)+2(a7+a9+a11)=24,则此数列的前13项之和为( )
| A. | 13 | B. | 26 | C. | 52 | D. | 156 |
11.函数$f(x)=\frac{-3+4x}{5-2x}$的值域是( )
| A. | (-∞,2)∪(2,+∞) | B. | (-∞,-2)∪(-2,+∞) | C. | $({-∞,\frac{5}{2}})∪({\frac{5}{2},+∞})$ | D. | R |
11.下列函数定义域是R且在区间(0,1)是递增函数的( )
| A. | y=|x+1| | B. | y=$\sqrt{x}$ | C. | y=$\frac{1}{x}$ | D. | y=-x2+4 |
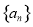 的前
的前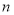 项和
项和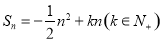 ,且
,且 的最大值为8.
的最大值为8.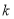 ,并求
,并求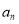 ;
;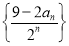 的前
的前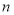 项和
项和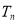 .
.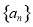 中,
中,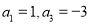 ,则
,则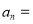 ____________.
____________.