题目内容
已知向量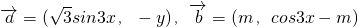 (m∈R),且
(m∈R),且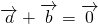 .设y=f(x).
.设y=f(x).
(1)求f(x)的表达式,并求函数f(x)在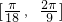 上图象最低点M的坐标.
上图象最低点M的坐标.
(2)若对任意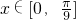 ,f(x)>t-9x+1恒成立,求实数t的范围.
,f(x)>t-9x+1恒成立,求实数t的范围.
解:(1)∵ ,即
,即 ,
,
消去m,得 ,
,
即 ,
,
 时,
时,
 ,
, ,
,
即f(x)的最小值为1,此时
∴函数f(x)的图象上最低点M的坐标是
(2)∵f(x)>t-9x+1,即 ,
,
当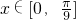 时,函数
时,函数 单调递增,y=9x单调递增,
单调递增,y=9x单调递增,
∴ 在
在 上单调递增,
上单调递增,
∴ 的最小值为1,
的最小值为1,
为要 恒成立,只要t+1<1,
恒成立,只要t+1<1,
∴t<0为所求.
分析:(1)根据所给的向量之间的关系,写出关于三角函数的关系式,消元得到函数式,整理成可以解决三角函数性质的形式,根据所给的变量的范围得到三角函数的范围.
(2)本题是一个函数的恒成立问题,写出关系式,分离参数,要证一个变量恒小于一个函数式时,要用一种函数思想,即只要这个变量小于函数的最小值即可.
点评:本题是一个三角函数同向量结合的问题,是以向量平行的充要条件为条件,得到三角函数的关系式,是一道综合题,在高考时可以以选择和填空形式出现.
 ,即
,即 ,
,消去m,得
 ,
,即
 ,
, 时,
时,
 ,
, ,
,即f(x)的最小值为1,此时

∴函数f(x)的图象上最低点M的坐标是

(2)∵f(x)>t-9x+1,即
 ,
,当
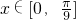 时,函数
时,函数 单调递增,y=9x单调递增,
单调递增,y=9x单调递增,∴
 在
在 上单调递增,
上单调递增,∴
 的最小值为1,
的最小值为1,为要
 恒成立,只要t+1<1,
恒成立,只要t+1<1,∴t<0为所求.
分析:(1)根据所给的向量之间的关系,写出关于三角函数的关系式,消元得到函数式,整理成可以解决三角函数性质的形式,根据所给的变量的范围得到三角函数的范围.
(2)本题是一个函数的恒成立问题,写出关系式,分离参数,要证一个变量恒小于一个函数式时,要用一种函数思想,即只要这个变量小于函数的最小值即可.
点评:本题是一个三角函数同向量结合的问题,是以向量平行的充要条件为条件,得到三角函数的关系式,是一道综合题,在高考时可以以选择和填空形式出现.

练习册系列答案
相关题目
已知向量集合M={
|
=(1,2)+λ(3,4),λ∈R},N={
|
=(-2,-2)+λ(4,5),λ∈R},则M∩N=( )
| a |
| a |
| a |
| a |
| A、{1,1} |
| B、{1,1,-2,-2} |
| C、{(-2,-2)} |
| D、∅ |
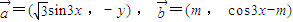 (m∈R),且
(m∈R),且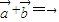 .设y=f(x).
.设y=f(x).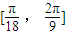 上图象最低点M的坐标.
上图象最低点M的坐标.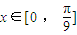 ,f(x)>t-9x+1恒成立,求实数t的范围.
,f(x)>t-9x+1恒成立,求实数t的范围.