题目内容
6.已知函数f(x)=$\frac{1}{2}$ax2+lnx-(a+1)x+$\frac{1}{2}$a(a为常数).(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在区间[1,+∞)的最小值为-1,求实数a的取值范围.
分析 (1)可确定函数f(x)的定义域为(0,+∞),求导f′(x)=2x+$\frac{1}{x}$-3=$\frac{(2x-1)(x-1)}{x}$,从而确定函数的单调区间;
(2)求导f′(x)=$\frac{(ax-1)(x-1)}{x}$,从而分类讨论以确定函数的单调性,从而求最值即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),
f(x)=x2+lnx-3x+1,f′(x)=2x+$\frac{1}{x}$-3=$\frac{(2x-1)(x-1)}{x}$,
当x>1时,f′(x)>0,当0<x<$\frac{1}{2}$时,f′(x)>0;
当$\frac{1}{2}$<x<1时,f′(x)<0;
故f(x)的单调减区间是($\frac{1}{2}$,1),单调增区间是(1,+∞)和(0,$\frac{1}{2}$);
(2)f′(x)=$\frac{(ax-1)(x-1)}{x}$,
当a≥1时,f′(x)>0,即f(x)在[1,+∞)上单调递增,所以f(x)≥f(1)=-1,
当0<a<1时,f(x)在(1,$\frac{1}{a}$)上单调递减,
所以,当x∈(1,$\frac{1}{a}$)时,f(x)≤f(1)=-1,不合题意,
当a≤0时,f′(x)<0,即f(x)在[1,+∞)上单调递减,
所以f(x)≤f(1)=-1,不合题意,
综上所述,实数a的取值范围是[1,+∞).
点评 本题考查了导数的综合应用及分类讨论的思想应用.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
14.动直线x=m(m>0)与函数f(x)=2x+$\frac{1}{x}$,g(x)=x-$\frac{1}{x}$-lnx分别交于点A,B,则|AB|的最小值为( )
| A. | 3+ln2 | B. | 2 | C. | $\frac{7}{2}$-ln2 | D. | 3 |
11.已知双曲线C:$\frac{{x}^{2}}{m+3}$-$\frac{{y}^{2}}{m}$=1(m>0)的渐近线方程为y=±$\frac{1}{2}$x,则双曲线C的焦距为( )
| A. | 1 | B. | 2$\sqrt{5}$ | C. | 3 | D. | 6 |
15.(文)设全集U=R,集合A={x|x2+4x<0},集合B={x|x<-2},则图中阴影部分表示的集合为( )
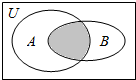

| A. | {x|-4<x<-2} | B. | {x|-4<x<0} | C. | {x|x>0} | D. | {x|x<-2} |
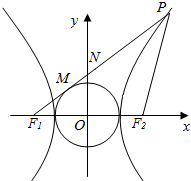 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P为双曲线右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则该双曲线的离心率e是$\frac{5}{3}$.
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P为双曲线右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则该双曲线的离心率e是$\frac{5}{3}$.