Question

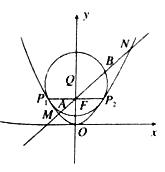
【题目】如图，抛物线的准线为，取过焦点且平行于轴的直线与抛物线交于不同的两点，过作圆心为的圆，使抛物线上其余点均在圆外，且．　

（Ⅰ）求抛物线和圆的方程；

（Ⅱ）过点作直线与抛物线和圆依次交于，求的最小值．

Answer 1

【答案】(1) ,;(2)16.

【解析】试题分析：（1）通过平面几何性质及圆锥曲线定义求轨迹方程；（2）借助勾股定理及弦长公式表示目标，然后利用二次函数求最值.

试题解析：

（Ⅰ） 因为抛物线的准线为;

所以解得，所以抛物线的方程为．

当时，由得： ，不妨设在左侧，则，

由题意设圆的方程为： ，

由且知： 　，　

∴是等腰直角三角形且，

∴　， ，则，

∴　圆的方程为： ．

（Ⅱ）由题意知直线的斜率存在,设直线的方程为: ，

圆心到直线的距离为: ，

∴．

由得： ，

设,由抛物线定义有: ，

∴，

设，则: 且，

∴　当即时, 的最小值为.