题目内容
已知数列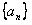 中,
中,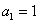 ,且点P
,且点P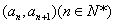 在直线x-y+1=0上。
在直线x-y+1=0上。
(1)求数列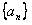 的通项公式;
的通项公式;
(2)设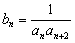 ,求数列
,求数列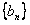 的前n项和Tn;
的前n项和Tn;
(3)设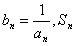 表示数列
表示数列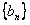 的前n项和。试问:是否存在关于n的整式
的前n项和。试问:是否存在关于n的整式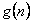 ,使得
,使得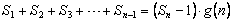 对于一切不小于2的自然数n恒成立? 若存在,写出
对于一切不小于2的自然数n恒成立? 若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
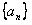 中,
中,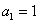 ,且点P
,且点P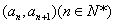 在直线x-y+1=0上。
在直线x-y+1=0上。(1)求数列
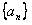 的通项公式;
的通项公式;(2)设
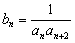 ,求数列
,求数列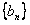 的前n项和Tn;
的前n项和Tn; (3)设
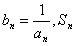 表示数列
表示数列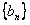 的前n项和。试问:是否存在关于n的整式
的前n项和。试问:是否存在关于n的整式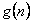 ,使得
,使得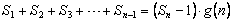 对于一切不小于2的自然数n恒成立? 若存在,写出
对于一切不小于2的自然数n恒成立? 若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。 解:(1)由点P 在直线x-y+1=0上,即
在直线x-y+1=0上,即 ,且
,且 ,
,
所以,数列{ }是以1为首项,1为公差的等差数列,
}是以1为首项,1为公差的等差数列,
∴ 。
。
(2) ,
,

 。
。
(3)由(1)知, ,
,
可得 ,
,
∴ ,
,
即 ,
,
∴ ,
,
 ,
,
…
 ,
,
∴ ,
,
即 ,n≥2,
,n≥2,
∴ ,
,
故存在关于n的整式 ,使得对于一切不小于2的自然数n恒成立。
,使得对于一切不小于2的自然数n恒成立。
 在直线x-y+1=0上,即
在直线x-y+1=0上,即 ,且
,且 ,
,所以,数列{
 }是以1为首项,1为公差的等差数列,
}是以1为首项,1为公差的等差数列,∴
 。
。(2)
 ,
,
 。
。(3)由(1)知,
 ,
,可得
 ,
,∴
 ,
,即
 ,
,∴
 ,
, ,
,…
 ,
,∴
 ,
,即
 ,n≥2,
,n≥2,∴
 ,
,故存在关于n的整式
 ,使得对于一切不小于2的自然数n恒成立。
,使得对于一切不小于2的自然数n恒成立。
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目