题目内容
在数列{an}中，a1=a，以后各项由递推公式
给出，写出这个数列的前4项：________、________、________、________，并由此写出一个通项公式an=________．
a 
分析：可根据递推公式写出数列的前4项，然后分析每一项与该项的序号之间的关系，归纳概括出an与n之间的一般规律，从而作出猜想，写出满足前4项的该数列的一个通项公式．
解答：∵a1=a，an+1=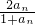
，∴a2=，
a3=
=
=，
a4=
=
=．
观察规律：an=
．
故答案为：a，，，；．
点评：从特殊的事例，通过分析、归纳、抽象总结出一般规律，再进行科学地证明，这是创新意识的具体体现，这种探索问题的方法，在解数列的有关问题中经常用到，应引起足够的重视．
分析：可根据递推公式写出数列的前4项，然后分析每一项与该项的序号之间的关系，归纳概括出an与n之间的一般规律，从而作出猜想，写出满足前4项的该数列的一个通项公式．
解答：∵a1=a，an+1=
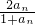，∴a2=，a3=
==，a4=
==．观察规律：an=
．故答案为：a，
，，；．点评：从特殊的事例，通过分析、归纳、抽象总结出一般规律，再进行科学地证明，这是创新意识的具体体现，这种探索问题的方法，在解数列的有关问题中经常用到，应引起足够的重视．
练习册系列答案
优加精卷系列答案
相关题目
，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=
（n∈N*）．
}的前n项和为Tn，证明：
．