Question

【题目】已知曲线： ， ： （），从上的点作轴的垂线，交于点，再从点作轴的垂线，交于点.设， ， .

（Ⅰ）求数列的通项公式；

（Ⅱ）记，数列的前项和为，求证： ；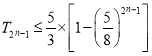

（Ⅲ）若已知（），记数列的前项和为，数列的前项和为，试比较与的大小.

Answer 1

【答案】（1） ；（2）见解析；（3）见解析.

【解析】试题分析：（1）依题意点的坐标为，则∴

从而能求出数列的通项公式．
（2）由，知，，当时， ，∴ ．由此能够证明；

（3）由∵，∴，由知（）

∴（），而，所以可得，

由此能够比较与的大小．

试题解析：（1）依题意点的坐标为，

∴∴

∴

.

（2）∵，所以： ，

∴当时， ，

∴ （当时取“”）.

（Ⅲ）∵，∴，

由知（）

∴（），而，所以可得，

于是

.

∴

当， 时， ；

当时，

当时，

∴当时，