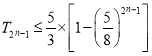题目内容
【题目】设函数![]() (
(![]() )
)
(Ⅰ)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)求![]() 单调区间;
单调区间;
(Ⅲ)若![]() 图象与
图象与![]() 轴关于
轴关于![]() ,
, ![]() 两点,求证:
两点,求证: ![]() .
.
【答案】(1)切线为![]() ;(2)
;(2)![]() 时
时![]() 在
在![]() 单增,
单增, ![]() 时
时![]() 在
在![]() 单减,
单减, ![]() 单增;(3)见解析.
单增;(3)见解析.
【解析】试题分析:(Ⅰ)当![]() 时
时![]() ,
, ![]() 因此切点为
因此切点为![]() ,求出
,求出![]() 利用点斜式可求切线方程;
利用点斜式可求切线方程;
(Ⅱ)求导![]() ,分类讨论可得
,分类讨论可得![]() 单调区间;
单调区间;
(Ⅲ)由(Ⅱ)可知![]() ,此时
,此时![]() 在在
在在![]() 单减,
单减, ![]() 单增,
单增,
设![]() 而
而![]() ,因此
,因此![]() ,经讨论可知本题即证
,经讨论可知本题即证![]() ,即证
,即证![]() ,构造函数
,构造函数![]() (
(![]() )讨论其性质即可得
)讨论其性质即可得
试题解析:(Ⅰ) ![]() ,
, ![]() 因此切点为
因此切点为![]() ,
,
![]() ,因此
,因此![]() ,因此切线为
,因此切线为![]() .
.
(Ⅱ)![]()
![]() 时
时![]() 在
在![]() 单增,
单增,
![]() 时
时![]() 在
在![]() 单减,
单减, ![]() 单增.
单增.
(Ⅲ)由(Ⅱ)可知![]() ,此时
,此时![]() 在在
在在![]() 单减,
单减, ![]() 单增,
单增,
设![]() 而
而![]() ,因此
,因此![]()
本题即证![]() ,而
,而![]() ,∴
,∴![]() ,
, ![]() .
.
即证![]() ,即证
,即证![]() ,
,
设![]()
![]() (
(![]() )
)
![]() 因此
因此![]() 在
在![]() 单增,由于
单增,由于![]() 可得
可得![]() 即
即![]() ,
,
由于![]() 因此
因此![]()
∵![]() ,
, ![]() ,
, ![]() 在
在![]() 单增,
单增,
∴![]() ,∴
,∴![]() ,
,
∴![]()

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目