题目内容
已知a>1,函数f(x)=loga(x2-ax+2)在x∈[2,+∞)时的值恒为正.
(1)a的取值范围;
(2)记(1)中a的取值范围为集合A,函数g(x)=log2(tx2+2x-2)的定义域为集合B.若A∩B≠∅,求实数t的取值范围.
(1)a的取值范围;
(2)记(1)中a的取值范围为集合A,函数g(x)=log2(tx2+2x-2)的定义域为集合B.若A∩B≠∅,求实数t的取值范围.
(1)x2-ax+2>1在x∈[2,+∞)时恒成立.即a<x+
在x∈[2,+∞)时恒成立.
又函数x+
在[2,+∞)上是增函数,
所以(x+
)min=
,
从而1<a<
.(6分)
(2)A=(1,
),B={x|tx2+2x-2>0}.
由于A∩B≠∅,
所以不等式tx2+2x-2>0有属于A的解,
即t>
-
有属于A的解.(8分)
又1<x<
时,
<
<1,
所以
-
=2(
-
)2-
∈[-
,0).
故t>-
.(12分)
| 1 |
| x |
又函数x+
| 1 |
| x |
所以(x+
| 1 |
| x |
| 5 |
| 2 |
从而1<a<
| 5 |
| 2 |
(2)A=(1,
| 5 |
| 2 |
由于A∩B≠∅,
所以不等式tx2+2x-2>0有属于A的解,
即t>
| 2 |
| x2 |
| 2 |
| x |
又1<x<
| 5 |
| 2 |
| 2 |
| 5 |
| 1 |
| x |
所以
| 2 |
| x2 |
| 2 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故t>-
| 1 |
| 2 |

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
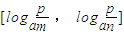 ,求实数p的取值范围;
,求实数p的取值范围;