Question

已知a＞1，函数f（x）的图象与函数y=a^x-1的图象关于直线y=x对称，g（x）=log_a（x²-2x+2）．
（1）求函数f（x）的解析式；
（2）若函数f（x）在区间[m，n]（n＞m＞-1）上的值域为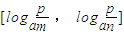，求实数p的取值范围；
（3）设函数F（x）=a^{f（x）-g（x）}，若w≥F（x）对一切x∈（-1，+∞）恒成立，求实数w的取值范围．

Answer 1

【答案】分析：（1）由函数f（x）的图象与函数y=a^x-1的图象关于直线y=x对称，知函数y=f（x）是函数y=a^x-1的反函数，从而可解．
（2）利用f（x）=log_a（x+1）在（-1，+∞）上是增函数，可得 ，，从而可转化为关于x的方程x²+x-p=0在（-1，0）∪（0，1）有两个不同的解，故可解．
（3）将w≥F（x）对一切x∈（-1，+∞）恒成立，转化为w≥F（x）_max，从而求函数的最大值即可．
解答：解：（1）由题意，函数y=f（x）是函数y=a^x-1的反函数，…（2分）
所以f（x）=log_a（x+1）（a＞1，x＞-1）．…（4分）
（2）因为a＞1，所以f（x）=log_a（x+1）在（-1，+∞）上是增函数，所以，，…（6分）
即，（n＞m＞-1且m≠0，n≠0），…（7分）
即m、n是方程（x∈（-1，0）∪（0，+∞））的两个不同解．…（8分）
即关于x的方程x²+x-p=0在（-1，0）∪（0，1）有两个不同的解．
所以，解得．
（3），…（12分）
令t=x+1，t＞0，则x=t-1，于是=，…（14分）
因为t＞0，所以，当且仅当时取等号．…（15分）
所以．                 …（16分）
因为w≥F（x）对一切x∈（-1，+∞）恒成立，所以w≥F（x）_max，…（17分）
因此w的取值范围是．                    …（18分）
点评：本题以反函数为依托，考查函数的解析式，研究函数的值域及恒成立问题，考查学生分析解决问题的能力．