题目内容
已知a>1,函数f(x)=loga(x2-ax+2)在x∈[2,+∞)时的值恒为正.(1)a的取值范围;
(2)记(1)中a的取值范围为集合A,函数g(x)=log2(tx2+2x-2)的定义域为集合B.若A∩B≠∅,求实数t的取值范围.
分析:(1)欲使x2-ax+2>1在x∈[2,+∞)时恒成立,转化成a<x+
在x∈[2,+∞)时恒成立,根据
函数x+
在[2,+∞)上的单调性求出最小值即可,使a小于最小值即可,注意条件a>1;
(2)先求出集合A,表示出集合B,根据A∩B≠∅,得不等式tx2+2x-2>0有属于A的解,即t>
-
有属于A的解,根据二次函数的性质求出
-
的值域,即可求出t的范围.
| 1 |
| x |
函数x+
| 1 |
| x |
(2)先求出集合A,表示出集合B,根据A∩B≠∅,得不等式tx2+2x-2>0有属于A的解,即t>
| 2 |
| x2 |
| 2 |
| x |
| 2 |
| x2 |
| 2 |
| x |
解答:解:(1)x2-ax+2>1在x∈[2,+∞)时恒成立.即a<x+
在x∈[2,+∞)时恒成立.
又函数x+
在[2,+∞)上是增函数,
所以(x+
)min=
,
从而1<a<
.(6分)
(2)A=(1,
),B={x|tx2+2x-2>0}.
由于A∩B≠∅,
所以不等式tx2+2x-2>0有属于A的解,
即t>
-
有属于A的解.(8分)
又1<x<
时,
<
<1,
所以
-
=2(
-
)2-
∈[-
,0).
故t>-
.(12分)
| 1 |
| x |
又函数x+
| 1 |
| x |
所以(x+
| 1 |
| x |
| 5 |
| 2 |
从而1<a<
| 5 |
| 2 |
(2)A=(1,
| 5 |
| 2 |
由于A∩B≠∅,
所以不等式tx2+2x-2>0有属于A的解,
即t>
| 2 |
| x2 |
| 2 |
| x |
又1<x<
| 5 |
| 2 |
| 2 |
| 5 |
| 1 |
| x |
所以
| 2 |
| x2 |
| 2 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故t>-
| 1 |
| 2 |
点评:本题主要考查了二次函数恒成立问题,以及函数的单调性等有关基础知识,同时考查了分析问题解决问题的能力,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
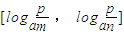 ,求实数p的取值范围;
,求实数p的取值范围;