题目内容
【题目】已知正项数列{an}的前n项和为Sn ， 数列{an}满足，2Sn=an（an+1）．
（1）求数列{an}的通项公式；
（2）设数列{ 
}的前n项和为An ， 求证：对任意正整数n，都有An＜ 
成立；
（3）数列{bn}满足bn=（ ）nan ， 它的前n项和为Tn ， 若存在正整数n，使得不等式（﹣2）n﹣1λ＜Tn+ 
﹣2n﹣1成立，求实数λ的取值范围．
【答案】
（1）解： 
，当n≥2时， 
，
两式相减得： 
，所以（an+an﹣1）（an﹣an﹣1﹣1）=0．
因为数列{an}为正项数列，故an+an﹣1≠0，也即an﹣an﹣1=1，
所以数列{an}为以1为首项1为公差的等差数列，故通项公式为an=n，n∈N*
（2）解： 
= 
，
所以对任意正整数n，都有 
成立
（3）解：易知 
，则 
，①，
，②
①﹣②可得： 
．
故 
，所以不等式 
成立，
若n为偶数，则 ，所以 
．
设 
，则y=﹣2t+t2+1=（t﹣1）2在 
单调递减，
故当 
时， 
，所以 
；
若n为奇数，则 
，所以 
．
设 
，则y=2t﹣t2﹣1=﹣（t﹣1）2在（0，1]单调递增，
故当t=1时，ymax=0，所以λ＜0．
综上所述，λ的取值范围λ＜0或
【解析】（1）根据数列的递推公式即可求出数列{an}的通项公式，（2） 
= 
＜ 
= 
﹣ 
，利用放缩法即可证明，（3）先利用错位相减法求出数列{bn}的前n项和为Tn ， 不等式（﹣2）n﹣1λ＜Tn+ 
﹣2n﹣1成立，转化为 成立，分n为偶数和奇数，根据函数的性质即可求出实数λ的取值范围
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系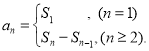
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
