题目内容
(本小题满分12分)
已知△ABC的内角A、B、C所对的边分别为 且
且 .
.
( I ) 若 ,求周长的最小值; (Ⅱ) 若
,求周长的最小值; (Ⅱ) 若 ,求边
,求边 的值.
的值.
解:(1)当且仅当 时,周长取到最小值为
时,周长取到最小值为 ;(2)
;(2)
解析试题分析:(1)根据三角形的面积公式和已知条件得到 ,
, 然后表示出周长l,结合均值不得等式得到最值。
然后表示出周长l,结合均值不得等式得到最值。
(2) ∵cosB= >0,且0<B<π,结合同角公式得到sinB,由正弦定理得
>0,且0<B<π,结合同角公式得到sinB,由正弦定理得 ,
,
解:(1) ,
, ,
, ,
,
当且仅当 时,周长取到最小值为
时,周长取到最小值为
(2) ∵cosB= >0,且0<B<π,∴sinB=
>0,且0<B<π,∴sinB=
由正弦定理得 ,
, ;
;
再由余弦定理得: 即
即 或
或 (舍去)
(舍去)
考点:本试题主要考查了运用正弦定理和余弦定理求解三角形的运用。
点评:解决该试题的关键是通过均值不等式得到周长的最小值。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
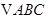 的内角
的内角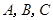 的对边分别是
的对边分别是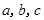 ,且
,且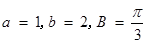 .
.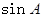 的值; (2) 求
的值; (2) 求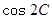 的值.
的值.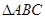 外接圆的半径为2,
外接圆的半径为2,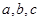 分别是
分别是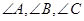 的对边
的对边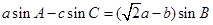
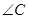 (2)求
(2)求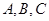 分别是锐角
分别是锐角 的三边
的三边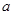 、
、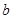 、
、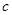 所对的角,
所对的角,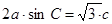 .
. 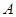 的大小;
的大小;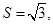 求
求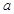 的最小值.
的最小值.
 ,P、Q分别是
,P、Q分别是 两边上的动点.
两边上的动点. ,
, 时,求PQ的长;(2)AP、AQ长度之和为定值4,求线段PQ最小值.
时,求PQ的长;(2)AP、AQ长度之和为定值4,求线段PQ最小值. 的内角,
的内角,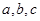 分别是其对边长,向量
分别是其对边长,向量 ,
, ,
, .
. 求
求 的长.
的长.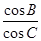 =-
=-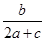 .
. 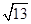 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积. x+2=0的两根,角A、B满足:2sin(A+B)-
x+2=0的两根,角A、B满足:2sin(A+B)-