题目内容
函数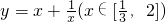 的最小值为________;最大值为________.
的最小值为________;最大值为________.
2 
分析:由题意函数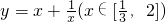 可以利用基本不等式的性质求函数的最小值,利用函数的增减性求出其最大值.
可以利用基本不等式的性质求函数的最小值,利用函数的增减性求出其最大值.
解答:∵函数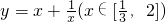
∴x+ ≥2(当且仅当x=1时等号成立)
≥2(当且仅当x=1时等号成立)
∵函数在( ,1)上为减函数,在(1,2)上为增函数,
,1)上为减函数,在(1,2)上为增函数,
∴f( )=3+
)=3+ =
= ,
,
f(2)= ,
,
故答案为:2, .
.
点评:此题考查不等式的基本性质及特殊函数的单调性,是一道好题.

分析:由题意函数
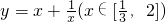 可以利用基本不等式的性质求函数的最小值,利用函数的增减性求出其最大值.
可以利用基本不等式的性质求函数的最小值,利用函数的增减性求出其最大值.解答:∵函数
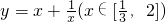
∴x+
 ≥2(当且仅当x=1时等号成立)
≥2(当且仅当x=1时等号成立)∵函数在(
 ,1)上为减函数,在(1,2)上为增函数,
,1)上为减函数,在(1,2)上为增函数,∴f(
 )=3+
)=3+ =
= ,
,f(2)=
 ,
,故答案为:2,
 .
.点评:此题考查不等式的基本性质及特殊函数的单调性,是一道好题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 的最小值为
的最小值为 ,最小正周期为16,且图象经过点(6,0)求这个函数的解析式.
,最小正周期为16,且图象经过点(6,0)求这个函数的解析式.