题目内容
已知函数 的最小值为
的最小值为 ,最小正周期为16,且图象经过点(6,0)求这个函数的解析式.
,最小正周期为16,且图象经过点(6,0)求这个函数的解析式.
【答案】分析:由函数最小值可得A,由周期为16可求ω,根据所过点(6,0)及φ的范围可得φ值.
解答:解:由题意可知: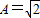 ,
,
由周期公式可得到: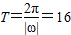 ,
,
又∵ω>0,∴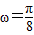 ,∴
,∴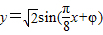 ,
,
又函数图象过点(6,0),
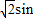 (
(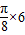 +φ)=0,即
+φ)=0,即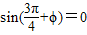 ,
,
又∵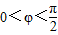 ,∴
,∴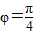 ,
,
所以函数解析式是: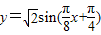 .
.
点评:本题考查由函数y=Asin(ωx+φ)的部分图象确定函数解析式,一般思路为:由函数最值确定A,由周期确定ω,由特殊点求出φ值.
解答:解:由题意可知:
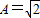 ,
,由周期公式可得到:
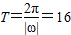 ,
,又∵ω>0,∴
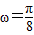 ,∴
,∴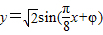 ,
,又函数图象过点(6,0),
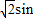 (
(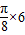 +φ)=0,即
+φ)=0,即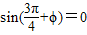 ,
,又∵
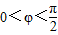 ,∴
,∴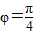 ,
,所以函数解析式是:
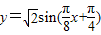 .
.点评:本题考查由函数y=Asin(ωx+φ)的部分图象确定函数解析式,一般思路为:由函数最值确定A,由周期确定ω,由特殊点求出φ值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 的最小值为0,其中
的最小值为0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的 有
有 ≤
≤ 成立,求实数
成立,求实数 的最小值;
的最小值;
(Ⅲ)证明 (
( ).
).
【解析】(1)解:
 的定义域为
的定义域为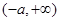

由 ,得
,得
当x变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
因此, 在
在 处取得最小值,故由题意
处取得最小值,故由题意 ,所以
,所以
(2)解:当 时,取
时,取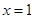 ,有
,有 ,故
,故 时不合题意.当
时不合题意.当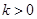 时,令
时,令 ,即
,即

令 ,得
,得
①当 时,
时, ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上单调递减.从而对于任意的
上单调递减.从而对于任意的 ,总有
,总有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合题意.
符合题意.
②当 时,
时, ,对于
,对于 ,
, ,故
,故 在
在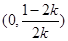 上单调递增.因此当取
上单调递增.因此当取 时,
时, ,即
,即 不成立.
不成立.
故 不合题意.
不合题意.
综上,k的最小值为 .
.
(3)证明:当n=1时,不等式左边= =右边,所以不等式成立.
=右边,所以不等式成立.
当 时,
时,


在(2)中取 ,得
,得
 ,
,
从而

所以有





综上,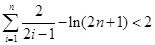 ,
,

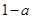


 的最小值为
的最小值为 ,则二项式
,则二项式 的展开式中常数项为第 项。
的展开式中常数项为第 项。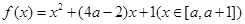 的最小值为
的最小值为 求函数
求函数 的解析式。
的解析式。