题目内容
函数y=x·e-x在x∈[2,4]上的最小值为( )
| A.0 | B. | C. | D. |
C
解析

练习册系列答案
相关题目
如图所示,曲线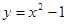 ,
, 围成的阴影部分的面积为( )
围成的阴影部分的面积为( )
A.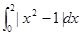 | B.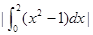 |
C. | D.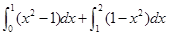 |
定义在R上的函数 满足
满足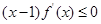 ,且
,且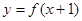 为偶函数,当
为偶函数,当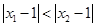 时,有( )
时,有( )
A.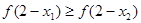 | B.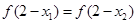 |
C.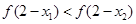 | D.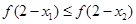 |
设函数f(x)= x3+
x3+ x2+tan θ,其中θ∈
x2+tan θ,其中θ∈ ,则导数f′(1)的取值范围是( )
,则导数f′(1)的取值范围是( )
| A.[-2,2] | B.[ , ,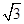 ] ] |
C.[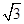 ,2] ,2] | D.[ ,2] ,2] |
已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为( )
| A.(-2,+∞) | B.(0,+∞) |
| C.(1,+∞) | D.(4,+∞) |
根据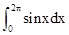 =0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
=0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
| A.面积为0 |
| B.曲边梯形在x轴上方的面积大于在x轴下方的面积 |
| C.曲边梯形在x轴上方的面积小于在x轴下方的面积 |
| D.曲边梯形在x轴上方的面积等于在x轴下方的面积 |
函数y=xlnx在区间(0,1)上是( )
| A.单调增函数 |
B.在(0, )上是减函数,在( )上是减函数,在( ,1)上是增函数 ,1)上是增函数 |
| C.单调减函数 |
D.在(0, )上是增函数,在( )上是增函数,在( ,1)上是减函数 ,1)上是减函数 |
函数y=cos(2x+1)的导数是( )
| A.y′=sin(2x+1) |
| B.y′=-2xsin(2x+1) |
| C.y′=-2sin(2x+1) |
| D.y′=2xsin(2x+1) |
设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1)时,f(x)=lo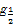 (1-x),则函数f(x)在(1,2)上( )
(1-x),则函数f(x)在(1,2)上( )
| A.是增函数,且f(x)<0 |
| B.是增函数,且f(x)>0 |
| C.是减函数,且f(x)<0 |
| D.是减函数,且f(x)>0 |