题目内容
如图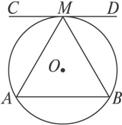
图
求证:(1)AB∥CD时,AM=MB.
(2)AM=MB时,AB∥CD.
证明:(1)∵AB∥CD,
∴∠A=∠AMC.
∵CD切⊙O于M,AM是弦,
∴∠AMC=∠B.∴∠A=∠B.
∴AM=BM.
(2)∵AM=MB,∴∠A=∠B.
又∵CD切⊙O于M,AM是弦,
∴∠AMC=∠B.∴∠AMC=∠A.
∴AB∥CD.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
题目内容
如图
图
求证:(1)AB∥CD时,AM=MB.
(2)AM=MB时,AB∥CD.
证明:(1)∵AB∥CD,
∴∠A=∠AMC.
∵CD切⊙O于M,AM是弦,
∴∠AMC=∠B.∴∠A=∠B.
∴AM=BM.
(2)∵AM=MB,∴∠A=∠B.
又∵CD切⊙O于M,AM是弦,
∴∠AMC=∠B.∴∠AMC=∠A.
∴AB∥CD.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案