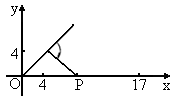Question

如图所示，根据指令(r，)(其中r≥0，－180°＜≤180°)，机器人在平面上能完成下列动作：先原地旋转角度(为正时，按逆时针方向旋转；为负时，按顺时针方向旋转－)，再朝面对的方向沿直线行走距离r．

(1)现机器人在直角坐标系的坐标原点，且面对x轴正方向．试给机器人下一个指令，使其移动到点A(4，4)．

(2)机器人在完成该指令后，发现在点(17，0)处有一小球正向坐标原点作匀速直线滚动．已知小球滚动的速度为机器人直线行走速度的2倍，若忽略机器人原地旋转所需的时间，问机器人最快可在何处截住小球？

Answer 1

答案：
解析：

解：(1)显然机器人必须沿着OA方向运动，故r＝|OA|＝，＝45°，即指令为(，45°)． 　　(2)设机器人最快在点P(x，0)处截住小球，则因为小球速度是机器人速度的2倍，所以在相同时间内有 　　|17－x|＝， 　　即3x2＋2x－161＝0，解得x＝(不合适，舍)或x＝7．因为要求机器人最快地去截住小球，即小球滚动距离最短，所以x＝7，故机器人最快可在点(7，0)处截住小球．