题目内容
设Sn是数列{an}的前n项和，点P（an，Sn）在直线y=2x-2上（n∈N+）。
（1）求数列{an}的通项公式；
（2）记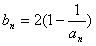
，数列{bn}的前n项和为Tn，求使Tn>2011的n的最小值；
（3）设正数数列{cn}满足log2an+1=（cn）n+1，求数列{cn}中的最大项。
（1）求数列{an}的通项公式；
（2）记
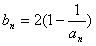，数列{bn}的前n项和为Tn，求使Tn>2011的n的最小值；（3）设正数数列{cn}满足log2an+1=（cn）n+1，求数列{cn}中的最大项。
解：（1）依题意得Sn=2an-2，则n≥2时
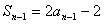
∴n≥2时
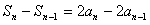
即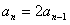
又n=1时，a1=2，
∴数列{an}是以a1=2为首项，以2为公比的等比数列，
∴an=2n。
（2）依题意
∴
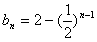
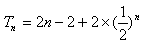
由Tn>2011，得
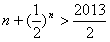
n≤1006（n∈N*）时
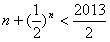
当n≥ 1007 （n∈N*）时
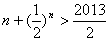
因此n的最小值为1007。
（3）由已知得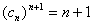
，即（n+1）lncn=ln（n+1），
∴
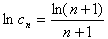
令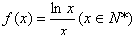
则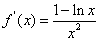
当x≥3时，lnx>1，即f'（x）＜0
∴f（x）在[3，+∞）上为递减函数
∴n≥2时，{lncn}是递减数列，即{cn}是递减数列，
c2>c3>c4>…>cn
∴c1＜c2>c3
∴c2为数列{cn}中最大项。
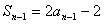
∴n≥2时
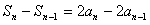
即
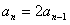
又n=1时，a1=2，
∴数列{an}是以a1=2为首项，以2为公比的等比数列，
∴an=2n。
（2）依题意
∴
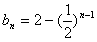
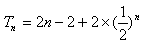
由Tn>2011，得
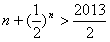
n≤1006（n∈N*）时
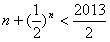
当n≥ 1007 （n∈N*）时
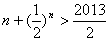
因此n的最小值为1007。
（3）由已知得
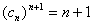，即（n+1）lncn=ln（n+1）， ∴
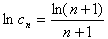
令
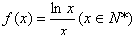
则
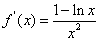
当x≥3时，lnx>1，即f'（x）＜0
∴f（x）在[3，+∞）上为递减函数
∴n≥2时，{lncn}是递减数列，即{cn}是递减数列，
c2>c3>c4>…>cn
∴c1＜c2>c3
∴c2为数列{cn}中最大项。
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目