题目内容
 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,且
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,且 .
.
(1)求该正四棱柱的体积;
(2)若E为线段A1D的中点,求异面直线BE与AA1所成角的大小.
解:(1)如图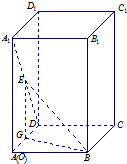
在正四棱柱ABCD-A1B1C1D1中,
∵AA1⊥平面ABCD,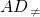 平面ABCD,
平面ABCD,
∴AA1⊥AD,故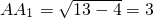 ,…(3分)
,…(3分)
∴正四棱柱的体积为(22)×3=12. …(6分)
(2)设G是棱AD中点,连GE,GB,在△A1AD中,
∵E,G分别为线段A1D,AD的中点,
∴EG∥A1A,且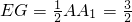 ,
,
∴∠GEB就是异面直线AA1与BE所成的角. …(8分)
∵A1A⊥平面ABCD,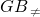 平面ABCD,∴AA1⊥GB,
平面ABCD,∴AA1⊥GB,
又EG∥A1A,∴EG⊥BG,…(10分)
∵ ,
,
∴ ,故
,故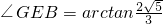 .
.
所以异面直线AA1与BE所成角的大小为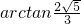 . …(12分)
. …(12分)
分析:(1)由题意可得AA1的长度,代入柱体的体积公式可得答案;(2)设G是棱AD中点,可得∠GEB就是异面直线AA1与BE所成的角,由三角形的知识可得 ,由反正切函数可得角的大小.
,由反正切函数可得角的大小.
点评:本题考查棱柱的体积,以及异面直线所成的角,涉及反三角函数的应用,属中档题.

在正四棱柱ABCD-A1B1C1D1中,
∵AA1⊥平面ABCD,
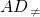 平面ABCD,
平面ABCD,∴AA1⊥AD,故
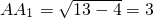 ,…(3分)
,…(3分)∴正四棱柱的体积为(22)×3=12. …(6分)
(2)设G是棱AD中点,连GE,GB,在△A1AD中,
∵E,G分别为线段A1D,AD的中点,
∴EG∥A1A,且
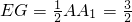 ,
,∴∠GEB就是异面直线AA1与BE所成的角. …(8分)
∵A1A⊥平面ABCD,
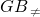 平面ABCD,∴AA1⊥GB,
平面ABCD,∴AA1⊥GB,又EG∥A1A,∴EG⊥BG,…(10分)
∵
 ,
,∴
 ,故
,故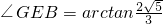 .
.所以异面直线AA1与BE所成角的大小为
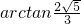 . …(12分)
. …(12分)分析:(1)由题意可得AA1的长度,代入柱体的体积公式可得答案;(2)设G是棱AD中点,可得∠GEB就是异面直线AA1与BE所成的角,由三角形的知识可得
 ,由反正切函数可得角的大小.
,由反正切函数可得角的大小.点评:本题考查棱柱的体积,以及异面直线所成的角,涉及反三角函数的应用,属中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
 如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为
如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为 如图,已知正四棱柱ABCD-A1B1C1D1与它的侧视图(或称左视图),E是DD1上一点,AE⊥B1C.
如图,已知正四棱柱ABCD-A1B1C1D1与它的侧视图(或称左视图),E是DD1上一点,AE⊥B1C. (2006•广州模拟)已知正四棱柱ABCD-A1B1C1D1,AB=BC=1,AA1=2,点E为CC1的中点,点F为BD1的中点.
(2006•广州模拟)已知正四棱柱ABCD-A1B1C1D1,AB=BC=1,AA1=2,点E为CC1的中点,点F为BD1的中点.