题目内容
下列结论正确的有
①y=x+
的最小值为2 ②当x>0且x≠1时,lgx+
≥2 ③y=
的最小值为2
④当x>0时,
+
≥2 ⑤y=sin2x+
,x∈(0,
)的最小值为2
⑥当x≥2时,x+
的最小值为2 ⑦y=x2+
的最小值为2.
④⑦
④⑦
①y=x+
| 1 |
| x |
| 1 |
| lgx |
| x2+3 | ||
|
④当x>0时,
| x |
| 1 | ||
|
| 1 |
| sin2x |
| π |
| 2 |
⑥当x≥2时,x+
| 1 |
| x |
| 1 |
| x2 |
分析:利用均值定理求最值要注意满足三个条件即一“正”;两个正数的算术平均数和几何平均数;二“定”:和是定值或积是定值;三“等号”:即等号成立的条件要具备,分别用这三个条件检验各选项即可
解答:解:若x<0则y=x+
<0,故①错误;若0<x<1,则lgx<0,lgx+
< 0,故②错误;y=
=
=
+
,由于
=
无解,故其最小值不为2,故③错误;当x>0时,
+
≥2
=2,故④正确;y=sin2x+
x∈(0,
),由于sin2x=
在x∈(0,
)上无解,故其最小值不为2,故⑤错误;当x≥2时,x=
无解,故其最小值不为2,故⑥错误;y=x2+
≥2
=2,故⑦正确
故答案为④⑦
| 1 |
| x |
| 1 |
| lgx |
| x2+3 | ||
|
| x2+2+1 | ||
|
| x2+2 |
| 1 | ||
|
| x2+2 |
| 1 | ||
|
| x |
| 1 | ||
|
|
| 1 |
| sin2x |
| π |
| 2 |
| 1 |
| sin2x |
| π |
| 2 |
| 1 |
| x |
| 1 |
| x2 |
x2•
|
故答案为④⑦
点评:本题考察了均值定理求最值的方法,解题时一定要牢记口诀一“正”二“定”三“等号”,并能熟练运用这些条件判断解题的正误

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
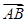 +
+ +
+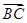 +
+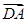 =a,而b是一非零向量,则下列结论正确的有( )
=a,而b是一非零向量,则下列结论正确的有( )