题目内容
6.在△ABC中,已知a:b:c=2:$\sqrt{6}$:($\sqrt{3}$+1)且△ABC的周长为3(1+$\sqrt{2}$+$\sqrt{3}$),解此三角形.分析 由已知可设a=2k,b=$\sqrt{6}k$,c=($\sqrt{3}$+1)k,(k>0),结合△ABC的周长为3(1+$\sqrt{2}$+$\sqrt{3}$)求得k值,即可得到三边长,再由余弦定理的推论求得角A和角B,结合三角形内角和定理求得C.
解答 解:在△ABC中,∵a:b:c=2:$\sqrt{6}$:($\sqrt{3}$+1),
∴可设a=2k,b=$\sqrt{6}k$,c=($\sqrt{3}$+1)k,(k>0),
由△ABC的周长为3(1+$\sqrt{2}$+$\sqrt{3}$),得2k+$\sqrt{6}k+\sqrt{3}k+k$=3(1+$\sqrt{2}$+$\sqrt{3}$),
即k=$\sqrt{3}$.
∴△ABC的三边长分别为:a=$2\sqrt{3}$,b=$3\sqrt{2}$,c=3+$\sqrt{3}$.
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{(3\sqrt{2})^{2}+(3+\sqrt{3})^{2}-(2\sqrt{3})^{2}}{2×3\sqrt{2}×(3+\sqrt{3})}$=$\frac{\sqrt{2}}{2}$,∴A=$\frac{π}{4}$.
cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{(2\sqrt{3})^{2}+(3+\sqrt{3})^{2}-(3\sqrt{2})^{2}}{2×2\sqrt{3}×(3+\sqrt{3})}$=$\frac{1}{2}$,∴B=$\frac{π}{3}$.
则C=π-$\frac{π}{4}-\frac{π}{3}=\frac{5π}{12}$.
点评 本题主要考查正弦定理、余弦定理的应用,三角形的内角和公式,解三角形,体现了分类讨论的数学思想,属于中档题.

| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
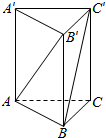 如图,在正三棱柱ABC-A′B′C′中,若AA′=2AB,则异面直线AB′与BC′所成角的余弦值为( )
如图,在正三棱柱ABC-A′B′C′中,若AA′=2AB,则异面直线AB′与BC′所成角的余弦值为( )| A. | 0 | B. | $\frac{3}{8}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
| A. | 本市明天将有70%的地区降雨 | B. | 本市明天将有70%的时间降雨 | ||
| C. | 明天出行带雨具的可能性很大 | D. | 明天出行不带雨具肯定要淋雨 |