题目内容
17.设函数f(x)=|lg(x+1)|,实数a,b(a<b)满足f(a)=f(-$\frac{b+1}{b+2}$),f(10a+6b+21)=4lg2,则a+b的值为-$\frac{11}{15}$.分析 根据题目给出的等式f(a)=f(-$\frac{b+1}{b+2}$),代入函数解析式得到a、b的关系,从而判断出f(10a+6b+21)的符号,再把f(10a+6b+21)=4lg2,转化为含有一个字母的式子即可求解.
解答 解:因为f(a)=f(-$\frac{b+1}{b+2}$),所以|lg(a+1)|=|lg(-$\frac{b+1}{b+2}$+1)|=|lg($\frac{1}{b+2}$)|=|lg(b+2)|,
所以a+1=b+2,或(a+1)(b+2)=1,又因为a<b,所以a+1≠b+2,所以(a+1)(b+2)=1.
又由f(a)=|lg(a+1)|有意义知a+1>0,从而0<a+1<b+1<b+2,
于是0<a+1<1<b+2.
所以(10a+6b+21)+1=10(a+1)+6(b+2)=6(b+2)+$\frac{10}{b+2}$>1.
从而f(10a+6b+21)=|lg[6(b+2)+$\frac{10}{b+2}$]|=lg[6(b+2)+$\frac{10}{b+2}$].
又f(10a+6b+21)=4lg2,
所以lg[6(b+2)+$\frac{10}{b+2}$]=4lg2,
故6(b+2)+$\frac{10}{b+2}$=16.解得b=-$\frac{1}{3}$或b=-1(舍去).
把b=-$\frac{1}{3}$代入(a+1)(b+2)=1解得a=-$\frac{2}{5}$.
所以 a=-$\frac{2}{5}$,b=-$\frac{1}{3}$.
a+b=-$\frac{11}{15}$.
故答案为:-$\frac{11}{15}$.
点评 本题考查了函数解析式的求解及常用方法,考查了数学代换思想,解答此题的关键是根据第一个等式找出a和b之间的关系,然后把一个字母用另一个字母代替,借助于第二个等式求解.

| A. | 已知 a,b,m∈R,命题“若 am2<bm2,则a<b”为真命题 | |
| B. | 命题“$?{x_0}∈R,{x_0}^2-{x_0}>0$”的否定是:“?x∈R,x2-x≤0” | |
| C. | 命题“p且q”为真命题,则命题p和q命题均为真命题 | |
| D. | “x>3”是“x>2”的充分不必要条件 |
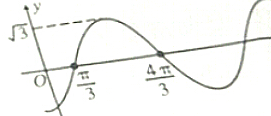 设函数f(x)=Asin(ωx+φ)x∈R,ω>0,|φ|<π),其导函数y=f′(x)的部分图象如图所示,
设函数f(x)=Asin(ωx+φ)x∈R,ω>0,|φ|<π),其导函数y=f′(x)的部分图象如图所示,