Question

6．若定义在R上的函数y=f（x）满足f（x+1）=$\frac{1}{f（x）}$且当x∈（0，1]时，f（x）=x，函数g（x）=$\left\{\begin{array}{l}{lo{g}_{3}x（x＞0）}\\{{2}^{x+1}（x≤0）}\end{array}\right.$，则函数h（x）=f（x）-g（x）在区间[-4，4]内的零点个数为5．

Answer 1

分析 函数h（x）=f（x）-g（x）在区间[-4，4]内的零点个数可转化为函数f（x）与g（x）的图象的交点的个数，从而作图求解．

解答 解：∵函数y=f（x）满足f（x+1）=$\frac{1}{f（x）}$，
∴f（x+2）=$\frac{1}{f（x+1）}$=f（x），
∴f（x）是周期为2的周期函数，
函数h（x）=f（x）-g（x）在区间[-4，4]内的零点个数可转化为函数f（x）与g（x）的图象在区间[-4，4]内的交点的个数，
作函数f（x）与g（x）在区间[-4，4]内的图象如下，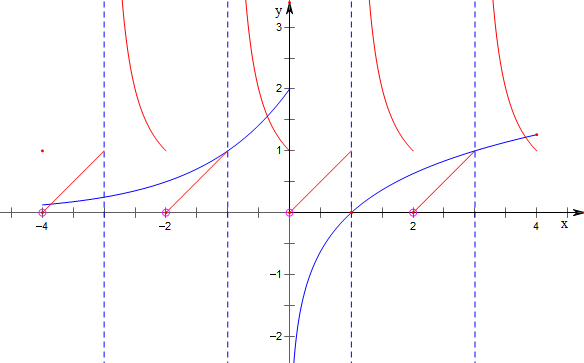

结合图象可知，共有5个交点，
故答案为：5．

点评 本题考查了分段函数的应用及函数的性质的判断与应用．