题目内容
曲线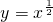 在点P(x0,y0)(0≤x0≤1)处的切线与x=0,x=1及x轴围成图形的面积的最小值为
在点P(x0,y0)(0≤x0≤1)处的切线与x=0,x=1及x轴围成图形的面积的最小值为
- A.1
- B.2
- C.

- D.

D
分析:由导数求出点P(x0,f(x0))(其中x0<0)处的切线为l的方程,求出直线与x=0,x=1及x轴的交点坐标,将面积S表示出的函数,再利用函数的单调性研究它的最值.
解答: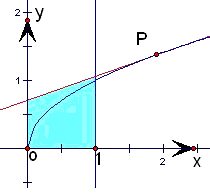 解:因为
解:因为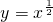 ,
,
∴y′=
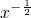 .
.
所以曲线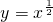 在点P处切线为l:
在点P处切线为l: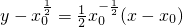 .…(6分)
.…(6分)
切线l与x=1的交点为(1,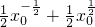 ),
),
与y轴的交点为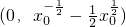 ,…(8分)
,…(8分)
因为0≤x0≤1,
所以S=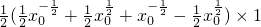
=
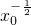 ,
,
∵在区间0,1]上,函数S(x0)单调递递减.…(10分)
所以,当x0=1时,S有最小值,此时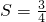 ,
,
所以,S的最小值为 .…(12分)
.…(12分)
故选D.
点评:本题考查利用导数研究曲线上某点切线方程、函数的最值等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:由导数求出点P(x0,f(x0))(其中x0<0)处的切线为l的方程,求出直线与x=0,x=1及x轴的交点坐标,将面积S表示出的函数,再利用函数的单调性研究它的最值.
解答:
 解:因为
解:因为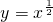 ,
,∴y′=

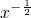 .
.所以曲线
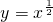 在点P处切线为l:
在点P处切线为l: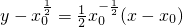 .…(6分)
.…(6分)切线l与x=1的交点为(1,
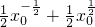 ),
),与y轴的交点为
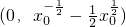 ,…(8分)
,…(8分)因为0≤x0≤1,
所以S=
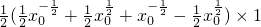
=

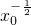 ,
,∵在区间0,1]上,函数S(x0)单调递递减.…(10分)
所以,当x0=1时,S有最小值,此时
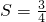 ,
,所以,S的最小值为
 .…(12分)
.…(12分)故选D.
点评:本题考查利用导数研究曲线上某点切线方程、函数的最值等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目