题目内容
如图求证:DE⊥AC.
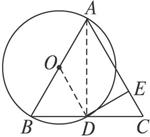
图
证明:连结OD、AD,
∵AB为⊙O直径,
∴AD⊥BC.
∵AB=AC,即△ABC为等腰三角形,
∴AD为BC边中线,即BD=DC.
又OA=OB,
∴OD为△ABC中位线.
∴OD∥AC.
∵DE切⊙O于D,∴OD⊥DE.
∴DE⊥AC.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
题目内容
如图求证:DE⊥AC.

图
证明:连结OD、AD,
∵AB为⊙O直径,
∴AD⊥BC.
∵AB=AC,即△ABC为等腰三角形,
∴AD为BC边中线,即BD=DC.
又OA=OB,
∴OD为△ABC中位线.
∴OD∥AC.
∵DE切⊙O于D,∴OD⊥DE.
∴DE⊥AC.

 初中暑期衔接系列答案
初中暑期衔接系列答案