题目内容
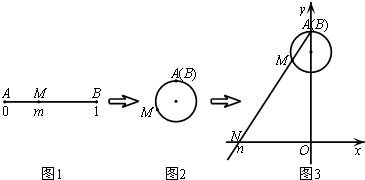
(2012•河北区一模)如图展示了一个由区间(0,1)到实数集R的映射过程:如图1,在区间(0,1)中数轴上的点M对应实数m;如图2,将线段AB围成一个圆,使两端点A、B恰好重合;如图3,将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),射线AM与x轴交于点N(n,0).则n就是m的象,记作f(m)=n.
下列说法:
①f(x) 的定义域为(0,1),值域为R;
②f(x) 是奇函数;
③f(x) 在定义域上是单调函数;
④f(
)=-
;
⑤f(x) 的图象关于点(
,0)对称.
其中正确命题的序号是

下列说法:
①f(x) 的定义域为(0,1),值域为R;
②f(x) 是奇函数;
③f(x) 在定义域上是单调函数;
④f(
| 1 |
| 4 |
| 1 |
| 2 |
⑤f(x) 的图象关于点(
| 1 |
| 2 |
其中正确命题的序号是
①③⑤
①③⑤
.(写出所有正确命题的序号)分析:①通过M点的运动轨迹以及直线的变化可求定义域和值域.
②由定义域不关于原点对称,可判断函数不是奇函数.
③在圆上,当点M在圆上运动时,N由x的负半轴向正半轴运动时,可判断函数的单调性.
④当m=
时,此时M恰好处在左半圆弧的中点上,此时可以求出对应直线AM的方程,进而可求n.
⑤根据点M的运动过程,可知函数的对称性.
②由定义域不关于原点对称,可判断函数不是奇函数.
③在圆上,当点M在圆上运动时,N由x的负半轴向正半轴运动时,可判断函数的单调性.
④当m=
| 1 |
| 4 |
⑤根据点M的运动过程,可知函数的对称性.
解答:解:①因为图中展示了一个由区间(0,1)到实数集R的映射过程,所以函数的定义域为(0,1),值域为R.所以①正确.
②由①知函数的定义域为(0,1),关于原点不对称,所以函数f(x)为非奇非偶函数,所以②错误.
③图3可以看出,m由0增大到1时,M由A运动到B,此时N由x的负半轴向正半轴运动,由此知,N点的横坐标逐渐变大,故f(x)在定义域上单调递增.所以③正确.
④因为AB=1,所以圆的周长为1,由2πr=1,所以解得圆的半径r=
,所以圆心坐标为(0,1-
).当m=
时,此时M恰好处在左半圆弧的中点上,此时M的坐标为(-
,1-
),对应直线AM的方程为y=x+1.当y=0,时,解得x=-1,即N(-1,0),所以n=-1,即f(
)=-1.所以④错误.
⑤图3可以看出,当M点的位置离中间位置相等时,N点关于y轴对称,即此时函数值互为相反数,故可知f(x)的图象关于点(
,0)对称,所以⑤正确.
所以正确命题的序号是①③⑤.
故答案为:①③⑤
②由①知函数的定义域为(0,1),关于原点不对称,所以函数f(x)为非奇非偶函数,所以②错误.
③图3可以看出,m由0增大到1时,M由A运动到B,此时N由x的负半轴向正半轴运动,由此知,N点的横坐标逐渐变大,故f(x)在定义域上单调递增.所以③正确.
④因为AB=1,所以圆的周长为1,由2πr=1,所以解得圆的半径r=
| 1 |
| 2π |
| 1 |
| 2π |
| 1 |
| 4 |
| 1 |
| 2π |
| 1 |
| 2π |
| 1 |
| 4 |
⑤图3可以看出,当M点的位置离中间位置相等时,N点关于y轴对称,即此时函数值互为相反数,故可知f(x)的图象关于点(
| 1 |
| 2 |
所以正确命题的序号是①③⑤.
故答案为:①③⑤
点评:本题考查了函数的实际应用,考查学生的阅读和分析能力.本题难度较大,正确阅读题意知解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 (2012•河北区一模)已知有若干辆汽车通过某一段公路,从中抽取200辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间[60,70)上的汽车大约有
(2012•河北区一模)已知有若干辆汽车通过某一段公路,从中抽取200辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间[60,70)上的汽车大约有 (2012•河北区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=
(2012•河北区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB= (2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=
(2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=