题目内容
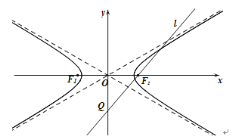
【题目】已知椭圆
：
（
）的一个焦点
与抛物线
：
的焦点重合，且离心率为
.
（1）求椭圆的标准方程；
（2）过焦点的直线
与抛物线交于
，
两点，与椭圆交于
，
两点，满足
，求直线的方程.
【答案】（1）
（2）
【解析】
（1）根据题意求出
，即可写出椭圆的标准方程.
（2）当直线
不存在斜率时，可求出
四点，可验证
；当直线存在斜率时，设直线方程为
，将直线分别与椭圆
方程、抛物线方程联立，利用弦长公式和焦点弦公式求出
、
，根据
解方程即可.
解：（1）由已知椭圆的离心率
，
，得
，则
，
故椭圆的标准方程为
（2）当直线不存在斜率时，可求出
，
，
，
，
所以
，
，不满足条件；
当直线存在斜率时，设直线方程为，代入椭圆方程得：
，
恒成立，
设
，
，则
∴
将直线：，代入抛物线
得
，
设
，
，则
，
又因为
，
由
得：
，∴
，
解得
，
所以直线的方程为.
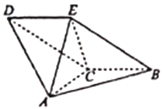
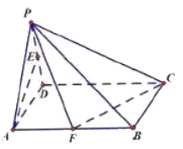
阅读快车系列答案
【题目】在平面直角坐标系中，
，设
的内切圆分别与边
相切于点
，已知
，记动点
的轨迹为曲线
.
(1)求曲线的方程;
(2)过
的直线与
轴正半轴交于点
，与曲线E交于点
轴，过的另一直线与曲线交于
两点，若
，求直线
的方程.
【题目】东莞的轻轨给市民出行带来了很大的方便，越来越多的市民选择乘坐轻轨出行，很多市民都会开汽车到离家最近的轻轨站，将车停放在轻轨站停车场，然后进站乘轻轨出行，这给轻轨站停车场带来很大的压力．某轻轨站停车场为了解决这个问题，决定对机动车停车施行收费制度，收费标准如下：4小时内（含4小时）每辆每次收费5元；超过4小时不超过6小时，每增加一小时收费增加3元；超过6小时不超过8小时，每增加一小时收费增加4元，超过8小时至24小时内（含24小时）收费30元；超过24小时，按前述标准重新计费．上述标准不足一小时的按一小时计费．为了调查该停车场一天的收费情况，现统计1000辆车的停留时间（假设每辆车一天内在该停车场仅停车一次），得到下面的频数分布表：
|
|
|
|
|
|
|
频数（车次） | 100 | 100 | 200 | 200 | 350 | 50 |
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率．
（1）现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研，记录并统计了停车时长与司机性别的
列联表：
男 | 女 | 合计 | |
不超过6小时 | 30 | ||
6小时以上 | 20 | ||
合计 | 100 |
完成上述列联表，并判断能否有90%的把握认为“停车是否超过6小时”与性别有关？
（2）（i）
表示某辆车一天之内（含一天）在该停车场停车一次所交费用，求的概率分布列及期望
；
（ii）现随机抽取该停车场内停放的3辆车，
表示3辆车中停车费用大于的车辆数，求
的概率．
参考公式：
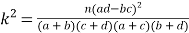，其中
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
