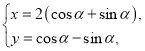题目内容
【题目】在平面直角坐标系中,![]() ,设
,设![]() 的内切圆分别与边
的内切圆分别与边![]() 相切于点
相切于点![]() ,已知
,已知![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与曲线E交于点
,与曲线E交于点![]() 轴,过
轴,过![]() 的另一直线与曲线
的另一直线与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】
(1)由内切圆的性质可知![]() ,
,![]() ,
,![]() ,转化
,转化![]() ,利用椭圆定义求椭圆方程;
,利用椭圆定义求椭圆方程;
(2)先求点![]() 的坐标,判断
的坐标,判断![]() ,再由
,再由![]() ,求得
,求得![]() ,所以
,所以![]() ,求得
,求得![]() ,再分斜率存在和斜率不存在两种情况,当斜率存在时,设直线
,再分斜率存在和斜率不存在两种情况,当斜率存在时,设直线![]() 与椭圆方程联立,得到根与系数的关系,并且根据
与椭圆方程联立,得到根与系数的关系,并且根据![]() 求斜率.
求斜率.
解:(1)由内切圆的性质可知![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]() .
.
所以曲线![]() 是以
是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆(除去与
的椭圆(除去与![]() 轴的交点).
轴的交点).
设曲线![]() 则
则![]() ,
,
即![]()
所以曲线![]() 的方程为
的方程为![]() .
.
(2)因为![]() 轴,所以
轴,所以![]() ,设
,设![]() ,
,
所以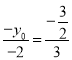 ,所以
,所以![]() ,则
,则![]()
因为![]() ,所以
,所以![]() ,
,
所以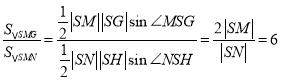
所以![]() ,所以
,所以![]()
设![]() 则
则![]()
![]() ,所以
,所以![]()
①直线![]() 斜率不存在时,
斜率不存在时, ![]() 方程为
方程为![]()
此时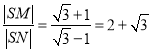 ,不符合条件舍去.
,不符合条件舍去.
②直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
联立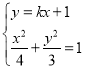 ,得
,得![]()
所以 ,
,
将![]() 代入得
代入得
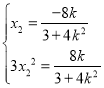 ,所以
,所以![]() .
.
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目