Question

过抛物线y²=2px（p＞0）准线上一点Q作抛物线的切线，分别切于A，B两点，则△ABQ的面积的最小值为（　　）

• A．2p²
• B．4p²
• C．

  p2

  2

• D．p²

Answer 1

分析：首先证明过抛物线y²=2px（p＞0）准线上一点Q作抛物线的两切线相互垂直，再证出过抛物线两垂直切线切点的连线恒过抛物线的焦点，进一步利用抛物线的性质与弦长公式把△ABQ的面积表示为弦AB倾斜角的函数，利用三角函数的值域求解△ABQ的面积的最小值．

解答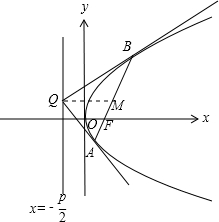：解：如图，设Q（-

p

2

，y0），过点Q与抛物线相切的直线方程为y-y0=k(x+

p

2

)（k≠0）．
联立

y-y0=k(x+ p 2 ) y2=2px

，得ky2-2py+2py0+kp2=0．
由△=(-2p)2-4k(2py0+kp2)=0．
得pk²+2y₀k-p=0．
由根与系数关系可得：k₁k₂=-1．
∴过Q点的抛物线的两条切线垂直．
再设A(

y12

2p

，y1)，B(

y22

2p

，y2)，则kAB=

y2-y1

y22 2p - y12 2p

=

2p

y2+y1

．
∴过A，B的直线方程为y-y1=

2p

y2+y1

(x-

y12

2p

)．
不妨设y₁＞0，y₂＜0．
由y=

2px

，得y′=

2

2

•

p x

，∴y′|x=x1=

p

y1

．
由y=-

2px

，得y′=-

2

2

•

p x

，∴y′|x=x2=

p

y2

．
由

p

y1

•

p

y2

=-1，得y1y2=-p2．
满足焦点弦两端点坐标的结论．
∴直线AB过抛物线的焦点F．
设直线AB与x轴的夹角为θ，由抛物线的性质可得：|AB|=

2p

sin2θ

．
且切线交点与弦中点的连线平行于坐标轴，设AB中点为M，
则|QM|=

1

2

|AB|=

p

sin2θ

．
Q到AB的距离为|QM|sinθ=

p

sin2θ

sinθ=

p

sinθ

．
∴S△ABQ=

1

2

|AB|•

p

sinθ

=

p2

sin3θ

．
当sinθ=1时，△ABQ的面积有最小值，最小值为p²．
故选D．

点评：本题考查了直线与圆锥曲线的关系，重点考查了抛物线的性质，该题涉及抛物线较多的性质，抛物线的性质较多，且推导过程过于复杂，学生应该把这些性质作为结论性的东西加以记忆，该题是有一定难度的题目．