题目内容
若关于x的方程x4+(a+1)x2+2a-4=0有两个不相等的实根,则实数a的取值范围是 .
考点:一元二次方程的根的分布与系数的关系
专题:综合题,不等式的解法及应用
分析:令x2=t,关于x的方程x4+(a+1)x2+2a-4=0有两个不相等的实根,可得t2+(a+1)t+2a-4=0有两个相等的正根,或有一个正根和一个负根,由此可得不等式组,即可求出实数a的取值范围.
解答:
解:令x2=t,
∵关于x的方程x4+(a+1)x2+2a-4=0有两个不相等的实根,
∴t2+(a+1)t+2a-4=0有两个相等的正根,或有一个正根和一个负根,
∴
或
,
∴a<2
∴实数a的取值范围为(-∞,2).
故答案为:(-∞,2).
∵关于x的方程x4+(a+1)x2+2a-4=0有两个不相等的实根,
∴t2+(a+1)t+2a-4=0有两个相等的正根,或有一个正根和一个负根,
∴
|
|
∴a<2
∴实数a的取值范围为(-∞,2).
故答案为:(-∞,2).
点评:本题考查一元二次方程的根的分布,考查学生分析解决问题的能力,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
若P={x|x<1},Q={x|x>-1},则( )
| A、∁RP⊆Q |
| B、Q⊆P |
| C、P⊆Q |
| D、Q⊆∁RP |
某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( )
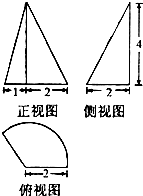

A、
| ||
B、
| ||
C、
| ||
D、
|
复数(
+
i)2的共轭复数是( )
| 1 |
| 2 |
| ||
| 2 |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|

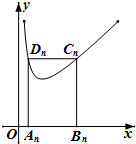 如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点CnDn在函数f(x)=x+
如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点CnDn在函数f(x)=x+