题目内容
5.过椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1的右焦点且倾斜角为$\frac{π}{3}$的直线被椭圆C截得的弦长为$\frac{4\sqrt{6}}{5}$.分析 由椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,可得右焦点F(2,0).设此直线的与椭圆相交于点A(x1,y1),B(x2,y2).直线方程为:y=$\sqrt{3}$(x-2).与椭圆方程联立化为:5x2-18x+15=0,利用|AB|=$\sqrt{4[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$即可得出.
解答 解:由椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,可得右焦点F(2,0).
设此直线的与椭圆相交于点A(x1,y1),B(x2,y2).
直线方程为:y=$\sqrt{3}$(x-2).
联立$\left\{\begin{array}{l}{y=\sqrt{3}(x-2)}\\{{x}^{2}+3{y}^{2}=6}\end{array}\right.$,
化为:5x2-18x+15=0,
∴x1+x2=$\frac{18}{5}$,x1x2=3.
∴|AB|=$\sqrt{4[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$2\sqrt{(\frac{18}{5})^{2}-4×3}$=$\frac{4\sqrt{6}}{5}$.
故答案为:$\frac{4\sqrt{6}}{5}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、弦长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.已知函数f(x)=|lgx|,0<a<b,且f(a)<f(b),则( )
| A. | ab=1 | B. | (a-1)(b-1)>0 | C. | ab<1 | D. | ab>1 |
14.已知全集∪=R,集合A={x|x≤0},B={x|x>-1},则集合A∩B=( )
| A. | {x|-1<x≤0} | B. | {x|-1≤x≤0} | C. | {x|x≤-1或x>0} | D. | {x|x≤-1或x≥0} |
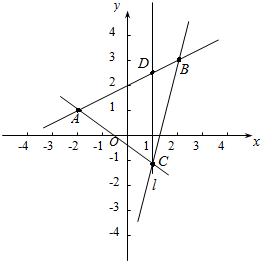 已知点A(-2,1),B(2,3),C(1,-1),直线l经过点C且与线段AB相交,求直线l的斜率的取值范围.
已知点A(-2,1),B(2,3),C(1,-1),直线l经过点C且与线段AB相交,求直线l的斜率的取值范围.