题目内容
抛物线y2=8x上有一点P(2,4),以P为一个顶点,作抛物线的内接△PQR,使得△PQR的重心是抛物线的焦点,求QR所在直线的方程.
2x+y-2=0.
解析:
设Q(x1,y1),R(x2,y2),则由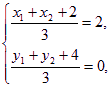 得
得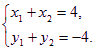
∴QR的中点为(2,-2).∵y12=8x1,y22=8x2,∴两式相减得(y1+y2)(y1-y2)=8(x1-x2),
即![]() =-2,即kQR=-2.
=-2,即kQR=-2.
∴QR:y+2=-2(x-2),即2x+y-2=0.

练习册系列答案
相关题目
题目内容
抛物线y2=8x上有一点P(2,4),以P为一个顶点,作抛物线的内接△PQR,使得△PQR的重心是抛物线的焦点,求QR所在直线的方程.
2x+y-2=0.
设Q(x1,y1),R(x2,y2),则由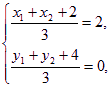 得
得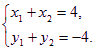
∴QR的中点为(2,-2).∵y12=8x1,y22=8x2,∴两式相减得(y1+y2)(y1-y2)=8(x1-x2),
即![]() =-2,即kQR=-2.
=-2,即kQR=-2.
∴QR:y+2=-2(x-2),即2x+y-2=0.
