题目内容
抛物线y2=8x上有一点P(2,4),以点P为一个顶点,作抛物线的内接△PQR,使得△PQR的重心恰好是抛物线的焦点,求QR所在直线的方程.
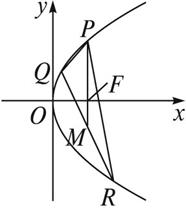
分析:P点恰好在焦点F(2,0)的正上方,因为F为△PQR的重心,所以QR的中点为M(2,-2),将该问题转化为已知QR的中点求弦所在直线方程的问题.
解:抛物线y2=8x的焦点为F(2,0).
∵F为△PQR的重心,
∴QR的中点为M(2,-2),如图.
设Q(x1,y1)、R(x2,y2),
则有

①-②,得y12-y22=8(x1-x2).
又y1+y2=-4,
∴直线QR的斜率为
![]()
∴所求弦QR所在直线的方程为
y+2=-2(x-2),
即2x+y-2=0.
绿色通道:
所谓“设而不求”就是解题时,把题目中某些相关的坐标先设出来,但在解题中并不求它的具体值,只要它作为解题过程中的“桥梁”,使问题快速获解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目