题目内容
若已知函数g（x）=
（x∈R）的值域为[2，8]，求实数m，n的值．
| mx2-3x+n |
| x2+1 |
考点：函数的值域
专题：计算题,函数的性质及应用
分析：函数g（x）=
（x∈R）的值域为[2，8]，可得，∴△=9-4（y-m）（y-n）≥0的解集为[2，8]．
| mx2-3x+n |
| x2+1 |
解答：
解：∵y=g（x）=
，
∴（y-m）x2+3x+y-n=0，
∵函数g（x）=
（x∈R）的值域为[2，8]，
∴△=9-4（y-m）（y-n）≥0的解集为[2，8]，
则9-4（2-m）（2-n）=0且9-4（8-m）（8-n）=0
解得，
或
．
| mx2-3x+n |
| x2+1 |
∴（y-m）x2+3x+y-n=0，
∵函数g（x）=
| mx2-3x+n |
| x2+1 |
∴△=9-4（y-m）（y-n）≥0的解集为[2，8]，
则9-4（2-m）（2-n）=0且9-4（8-m）（8-n）=0
解得，
|
|
点评：求值域的方法有多种，要根据条件选择一种较简单的方法．
练习册系列答案
相关题目
如图所示，已知P为⊙O外一点，A在⊙O上，PBC为割线，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且∠EDF=∠ECD．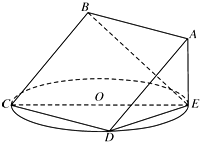
如图，正方形ABCD所在平面与圆O所在平面相交于CD，线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C、D的点．