题目内容
已知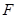 是椭圆
是椭圆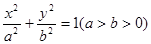 的左焦点,
的左焦点,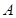 是椭圆短轴上的一个顶点,椭圆的离心率为
是椭圆短轴上的一个顶点,椭圆的离心率为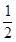 ,点
,点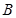 在
在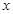 轴上,
轴上,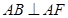 ,
,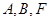 三点确定的圆
三点确定的圆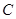 恰好与直线
恰好与直线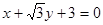 相切.
相切.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在过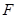 作斜率为
作斜率为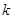
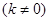 的直线
的直线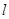 交椭圆于
交椭圆于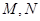 两点,
两点,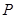 为线段
为线段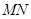 的中点,设
的中点,设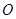 为椭圆中心,射线
为椭圆中心,射线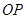 交椭圆于点
交椭圆于点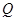 ,若
,若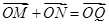 ,若存在求
,若存在求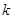 的值,若不存在则说明理由.
的值,若不存在则说明理由.
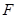 是椭圆
是椭圆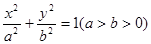 的左焦点,
的左焦点,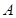 是椭圆短轴上的一个顶点,椭圆的离心率为
是椭圆短轴上的一个顶点,椭圆的离心率为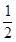 ,点
,点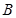 在
在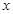 轴上,
轴上,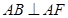 ,
,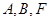 三点确定的圆
三点确定的圆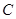 恰好与直线
恰好与直线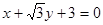 相切.
相切.(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在过
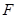 作斜率为
作斜率为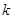
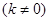 的直线
的直线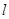 交椭圆于
交椭圆于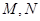 两点,
两点,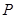 为线段
为线段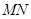 的中点,设
的中点,设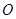 为椭圆中心,射线
为椭圆中心,射线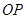 交椭圆于点
交椭圆于点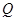 ,若
,若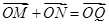 ,若存在求
,若存在求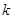 的值,若不存在则说明理由.
的值,若不存在则说明理由.20、解:





将(1)代入(2)可得:
(3+4k2)x2+8k2x+(4k2-12)="0 " 2’


3×64k4+4×36k2=12(4k2+3)2
64k4+48k2=4(16k4+24k2+9)
48k2 =96k2+36 2’
=96k2+36 2’
-48k2=36
∴k无解
∴不存在





将(1)代入(2)可得:
(3+4k2)x2+8k2x+(4k2-12)="0 " 2’


3×64k4+4×36k2=12(4k2+3)2
64k4+48k2=4(16k4+24k2+9)
48k2
 =96k2+36 2’
=96k2+36 2’-48k2=36
∴k无解
∴不存在
略

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 ,
, ,P在椭圆上,若 △
,P在椭圆上,若 △ 的面积的最大值为12,则椭圆方程为 ( )
的面积的最大值为12,则椭圆方程为 ( )



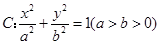 的中心在原点,它的左右两个焦点分别为
的中心在原点,它的左右两个焦点分别为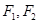 ,过右焦点
,过右焦点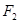 且与
且与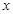 轴垂直的直线
轴垂直的直线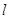 与椭圆
与椭圆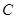 相交,其中一个交点为
相交,其中一个交点为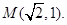
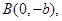 直线
直线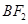 交椭圆
交椭圆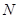 ,求
,求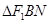 的面积.
的面积.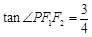 ,则椭圆的离心率为___________
,则椭圆的离心率为___________ 是椭圆的两焦点,
是椭圆的两焦点, 为椭圆上一点,若
为椭圆上一点,若 ,则离心率
,则离心率 的最小值是_______
的最小值是_______ 、
、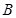 、
、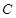 是椭圆
是椭圆 上的三个动点,若右焦点
上的三个动点,若右焦点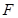 是
是 的重心,则
的重心,则
 的值是
的值是 的离心率为
的离心率为 ,右焦点到直线
,右焦点到直线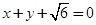 的距离为
的距离为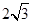 ,过
,过 的直线
的直线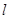 交椭圆于
交椭圆于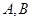 两点
两点 .
.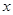 轴于
轴于 ,
,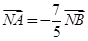 ,求直线
,求直线 的焦点坐标是( )
的焦点坐标是( )


