题目内容
如图所示,在四棱锥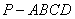 中,底面四边形
中,底面四边形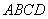 是菱形,
是菱形,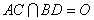 ,
,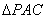 是边长为2的等边三角形,
是边长为2的等边三角形,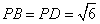 ,
,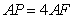 .
.
(Ⅰ)求证: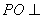 底面
底面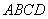 ;
;
(Ⅱ)求直线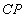 与平面
与平面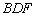 所成角的大小;
所成角的大小;
(Ⅲ)在线段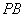 上是否存在一点
上是否存在一点 ,使得
,使得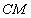 ∥平面
∥平面 ?如果存在,求
?如果存在,求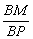 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.

解:(Ⅰ)因为底面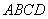 是菱形,
是菱形,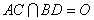 ,
,
所以 为
为 中点.
中点.
又因为 ,
,
所以 ,
,
所以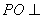 底面
底面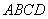 .
.

 (Ⅱ)由底面
(Ⅱ)由底面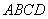 是菱形可得
是菱形可得 ,
,
又由(Ⅰ)可知 .
.
如图,以 为原点建立空间直角坐标系
为原点建立空间直角坐标系 .
.
由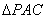 是边长为2的等边三角形,
是边长为2的等边三角形,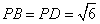 ,
,
可得 .
.
所以 .
.
所以 ,
, .
.
由已知可得
设平面 的法向量为
的法向量为 ,则
,则
 即
即
令 ,则
,则 ,所以
,所以 .
.
因为 ,
,
所以直线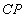 与平面
与平面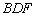 所成角的正弦值为
所成角的正弦值为 ,
,
所以直线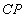 与平面
与平面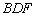 所成角的大小为
所成角的大小为 .
.
(Ⅲ)设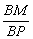

 ,则
,则
 .
.
若使 ∥平面
∥平面 ,需且仅需
,需且仅需 且
且 平面
平面 ,
,
解得 ,
,
所以在线段 上存在一点
上存在一点 ,使得
,使得 ∥平面
∥平面 .
.
此时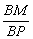 =
= .
.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
复数 ( )
( )
| A. | B. | C. | D. |
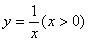 ,e是自然对数的底,则曲边梯形的面积是
,e是自然对数的底,则曲边梯形的面积是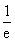 (D)
(D)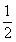
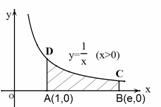
 椭圆的离心率
椭圆的离心率 ,命题
,命题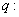 与抛物线只有一个公共点的直线是此抛物线的切线,那么 ( )
与抛物线只有一个公共点的直线是此抛物线的切线,那么 ( ) 是真命题 (B)
是真命题 (B)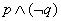 是真命题
是真命题 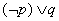 是真命题 (D)
是真命题 (D) 是假命题
是假命题 的展开式中的常数项为
的展开式中的常数项为  C.
C. D.
D. 
 与圆
与圆 相切于点
相切于点 ,过点
,过点 作圆
作圆 于
于 两点,
两点, ,
, ,则圆
,则圆




 的参数方程为
的参数方程为
 为参数
为参数 ,则圆
,则圆 的距离为______.
的距离为______.  满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, (B)
(B)  (C)
(C)  (D)
(D) 
 在
在 上的最大值、最小值分别是
上的最大值、最小值分别是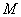 ,
,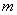 ,
,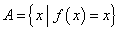 .
.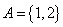 ,且
,且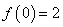 ,求
,求 ,且
,且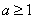 ,记
,记 ,求
,求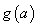 的最小值.
的最小值.