题目内容
已知f(x)=
+
，x∈(0，π).(1)将f(x)表示成cosx的多项式；
(2)求f(x)的最小值.
解：(1)f(x)=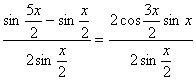=2coscos
=cos2x+cosx=2cos2x+cosx-1.
(2)∵f(x)=2(cosx+
)2-
，且-1≤cosx≤1，
∴当cosx=
时，f(x)取得最小值
.
练习册系列答案
相关题目
已知f(x)=sin(x+
)，g(x)=cos(x-
)，则下列结论中正确的是（ ）
| π |
| 2 |
| π |
| 2 |
| A、函数y=f（x）•g（x）的周期为2 | ||
| B、函数y=f（x）•g（x）的最大值为1 | ||
C、将f（x）的图象向左平移
| ||
D、将f（x）的图象向右平移
|