Question

    如图，在四棱锥ABCD-PGFE中，底面ABCD是直角梯形，侧棱垂直于底面，AB//DC，∠ABC＝45^o，DC＝1，AB＝2，PA＝1．

（Ⅰ）求PD与BC所成角的大小；

（Ⅱ）求证：BC⊥平面PAC；

（Ⅲ）求二面角A-PC-D的大小．

Answer 1

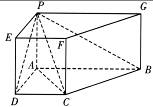
（Ⅰ）取的AB中点H，连接DH，易证BH//CD，且BD=CD …………………1分

        所以四边形BHDC为平行四边形，所以BC//DH

        所以∠PDH为PD与BC所成角………………………………………………2分

        因为四边形，ABCD为直角梯形，且∠ABC=45^o，  所以⊥DA⊥AB

        又因为AB=2DC=2，所以AD=1，  因为Rt△PAD、Rt△DAH、Rt△PAH都为等腰直角三角形，所以PD=DH=PH=，故∠PDH=60^o  ……………4分

   （Ⅰ）连接CH，则四边形ADCH为矩形， ∴AH=DC   又AB=2，∴BH=1

         在Rt△BHC中，∠ABC=45^o ， ∴CH=BH=1，CB=  ∴AD=CH=1，AC=

      ∴AC²+BC²=AB²    ∴BC⊥AC……6分 又PA平面ABCD∴PA⊥BC ……7分

∵PA∩AC=A∴BC⊥平面PAC  ………………………………………8分

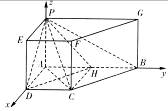   （Ⅲ）如图，分别以AD、AB、AP为x轴，y轴，z轴

建立空间直角坐标系，则由题设可知：

A(0，0，0)，P(0，0，1)，C(1，1，0)，D(1，0，0)，

         ∴=(0，0，1)，=(1，1，-1) ………………………………………… 9分

         设m=(a，b，c)为平面PAC的一个法向量，  则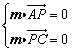，即

         设，则，∴m=(1，-1，0)  ………………………………………10分

         同理设n=(x，y，z) 为平面PCD的一个法向量，求得n=(1，1，1) ………11分

         ∴

         所以二面角A-PC-D为60^o