题目内容
某工厂2009年生产某种产品2万件,计划从2010年起每年比上一年增长20%,这个工厂年产量超过12万的最早的一年是(注:lg2=0.3010,lg3=0.4771)
| A.2018年 | B.2019年 | C.2020年 | D.2021年 |
B
解析试题分析:设a1为这家工厂2009年生产这种产品的年产量,即a1=2.
并将这家工厂,2010,2011年生产这种产品的年产量分别记为a2,a3,
根据题意,数列{an}是一个公比为1、2的等比数列,其通项公式为an=2×1.2n-1
根据题意,设2×1.2n-1=12两边取常用对数,得lg2+(x-1)lg1.2=lg12. .
.
因为y=2×1.2x是增函数,现x取正整数,可知从2019年开始,
这家工厂生产这种产品的产量超过12万台
考点:数列的应用.
点评:解数列应用题关键是看出是哪种数列类型,然后构造相应数列解决即可.

练习册系列答案
相关题目
已知等比数列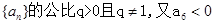 ,则 ( )
,则 ( )
A.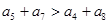 | B.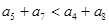 |
C.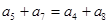 | D.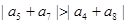 |
设 为等比数列
为等比数列 的前
的前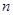 项和,已知
项和,已知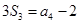 ,
,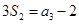 ,则公比
,则公比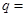 ( )
( )
| A.3 | B.4 | C.5 | D.6 |
在等比数列 中,
中, ,则数列
,则数列 的第4项为
的第4项为
A.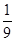 | B.81 | C.-81 | D.81或-81 |
数列 满足
满足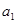 ,
,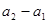 ,
, ,…,
,…,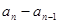 是首项为
是首项为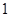 ,公比为
,公比为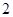 的等比数列,那么
的等比数列,那么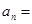 ( )
( )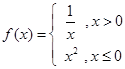
A.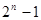 | B.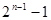  | C.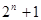 | D.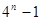 |
定义在 上的函数
上的函数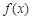 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
,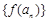 仍是等比数列,则称
仍是等比数列,则称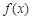 为“保等比数列函数”.现有定义在
为“保等比数列函数”.现有定义在 上的如下函数: ①
上的如下函数: ① ; ②
; ② ; ③
; ③ ; ④
; ④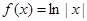 .
.
则其中是“保等比数列函数”的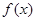 的序号为
的序号为
| A.①② | B.③④ | C.①③ | D.②④ |
已知等比数列 中,
中, ,则其前3项的和
,则其前3项的和 的取值范围是
的取值范围是
A. | B.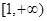 |
C.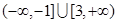 | D.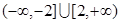 |
在等比数列 中,
中, =1,
=1, =3,则
=3,则 的值是 ( )
的值是 ( )
| A.14 | B. | C.18 | D.20 |
由数列1,10,100,1000,……猜测该数列的第 项可能是
项可能是 ( )
( )
A. | B. | C. | D. |