题目内容
定义在 上的函数
上的函数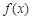 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
,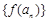 仍是等比数列,则称
仍是等比数列,则称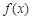 为“保等比数列函数”.现有定义在
为“保等比数列函数”.现有定义在 上的如下函数: ①
上的如下函数: ① ; ②
; ② ; ③
; ③ ; ④
; ④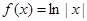 .
.
则其中是“保等比数列函数”的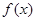 的序号为
的序号为
| A.①② | B.③④ | C.①③ | D.②④ |
C
解析试题分析:设等比数列 公比为q,首项为a1,则①
公比为q,首项为a1,则① ,所以数列
,所以数列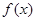 是等比数列,因而
是等比数列,因而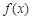 为“保等比数列函数”.
为“保等比数列函数”.
② ,
, ,显然不一定是等比数列.
,显然不一定是等比数列.
③ 一定是等比数列,所以数列
一定是等比数列,所以数列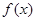 是等比数列,因而
是等比数列,因而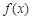 为“保等比数列函数”.
为“保等比数列函数”.
④ 不是常数.
不是常数.
所以其中是“保等比数列函数”的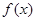 的序号为①③.
的序号为①③.
考点:新情景情况下分析问题解决问题的能力,等比数列的定义,及等比数列的通项公式.
点评:新情景,新定义是高考经常设置的题型,这种题型新而不难,但关键是正确理解题意,搞清其成立条件,再具有扎实的基础知识,这种题型不难解决.

练习册系列答案
相关题目
已知等比数列 的前
的前 项和为
项和为 ,
, ,则实数
,则实数 的值是
的值是
A. | B. | C. | D. |
已知数列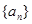 为等比数列,
为等比数列, ,
,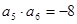 ,则
,则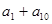 的值为( )
的值为( )
A.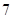 | B.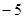 | C. | D.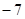 |
设 成等比数列,其公比为2,则
成等比数列,其公比为2,则 的值为( )
的值为( )
| A.1 | B. | C. | D. |
某工厂2009年生产某种产品2万件,计划从2010年起每年比上一年增长20%,这个工厂年产量超过12万的最早的一年是(注:lg2=0.3010,lg3=0.4771)
| A.2018年 | B.2019年 | C.2020年 | D.2021年 |
已知等比数列 的公比为正数,且
的公比为正数,且 ·
· =2
=2 ,
, =1,则
=1,则 =
=
A. | B. | C. | D. 2 |
等比数列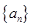 中,
中, 则
则 = ( )
= ( )
A. | B. | C. | D. |
已知各项均为正数的等比数列{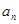 }中,
}中, =5,
=5, =10,则
=10,则
 =( )
=( )
A. | B.7 | C.6 | D. |
若m是2和8的等比中项,则圆锥曲线 的离心率是( )
的离心率是( )
A. | B. |
C. 或 或 | D. |