题目内容

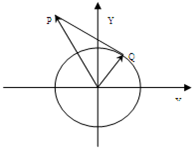精英家教网已知点P(-1，
3
)，O为原点，Q在圆x2+y2=1上，并且
OQ
•
QP
=0，则
OQ
+
OP
的长度为（　　）
分析：先求OP长，根据数量积为0得到OQ⊥QP，求出QP的长，然后取QP的中点为M，连接OM，根据勾股定理求出OM的长，最后根据向量的加法法则可知
OQ
+
OP
=2
OM
，从而可求出所求．
解答：解：∵P(-1，
3
)，
∴OP=
(-1-0)2+(
3
-0)2
=2
∵
OQ
•
QP
=0
∴OQ⊥QP而OQ=1
∴QP=
3

取QP的中点为M，连接OM，则OM=
(
3
2
)2+12
=
7
2

而
OQ
+
OP
=2
OM

∴
OQ
+
OP
的长度为
7

故选C．
点评：本题主要考查了平面向量数量积的运算，以及向量的模，同时考查了运算求解的能力，属于基础题．
练习册系列答案
相关题目
已知点（1，3）、（an，an+1）（n∈N*）都在函数f（x）=px+2（p为常数）的图象上，a1=1，数列{bn}满足：bn=an+
1n(n+1)
（n∈N*）．
（I）求数列{an}的通项公式；   
（II）求数列{bn}的前n项和Sn．

已知F1，F2分别为椭圆的上下焦点，其中F1也是抛物线C2：x2＝4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|＝．

(1)求椭圆C1的方程；

(2)已知点P(1，3)和圆O：x2＋y2＝b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足且λ≠±1．

求证：点Q总在某定直线上．

已知F1、F2分别为椭圆C1：的上、下焦点，其中F1也是抛物线C2：x2＝4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|＝．

(Ⅰ)求椭圆的方程；

(Ⅱ)已知点P(1，3)和圆O：x2＋y2＝b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB取一点Q，满足：＝－λ，＝λ(λ≠0且λ≠±1)．求证：点Q总在某定直线上．

如图，已知F1、F2分别为椭圆的上、下焦点，其中F1也是抛物线C2∶x2＝4y的焦点，点M是C1与C2在第二象限的交点，且

(I)求椭圆C1的方程；

(II)已知点P(1，3)和圆O∶x2＋y2＝b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足∶，(λ≠0且λ≠±1)，求证∶点Q总在某条定直线上．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网