Question

【题目】在平面直角坐标系xoy中，直线的参数方程为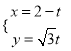（t为参数），P、Q分别为直线与x轴、y轴的交点，线段PQ的中点为M．

（Ⅰ）求直线的直角坐标方程；

（Ⅱ）以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标和直线OM的极坐标方程．

Answer 1

【答案】（Ⅰ）；（Ⅱ）M的极坐标为，直线OM的极坐标方程为：；

【解析】试题分析：（Ⅰ）直接根据直线的参数方程消去参数即可得出直角坐标下的直线的方程；（Ⅱ）分别令和计算出点P的直角坐标为（2,0）和点Q的直角坐标为.，由中点的坐标计算公式可得线段PQ的中点M的直角坐标为. 然后由极坐标与直角坐标的相互转化公式即可得出点M的极坐标为，于是直线OM的极坐标方程为：.

试题解析：（Ⅰ）由为参数）得，所以直线的平面直角坐标方程为.

（Ⅱ）当时，，所以点P的直角坐标为（2,0）；当时，，所以点Q的直角坐标为. 所以线段PQ的中点M的直角坐标为. 所以和，且

，，所以M的极坐标为，直线OM的极坐标方程为：.