题目内容
记函数fn(x)=(1+x)n-1(n≥2,n∈N*)的导函数为f 'n(x),函数g(x)=fn(x)-nx.
(Ⅰ)讨论函数g(x)的单调区间和极值;
(Ⅱ)若实数x0和正数k满足: ,求证:0<x0<k.
,求证:0<x0<k.
(Ⅰ)由已知得,g(x)=fn(x)-nx=(1+x)n-1-nx,∴g'(x)=n[(1+x)n-1-1].
①当n≥2且n是偶数时,n-1是奇数,
由g'(x)>0,得x>0;由g'(x)<0,得x<0.
∴函数g(x)的递减区间是(-∞,0),递增区间是(0,+∞),
故函数g(x)的极小值为g(0)=0,没有极大值.
②当n≥2且n是奇数时,n-1是偶数,
由g'(x)>0,得x<-2或x>0;由g'(x)<0,得-2<x<0.
∴函数g(x)的递增区间是(-∞,-2),(0,+∞),递减区间是(-2,0),
故函数g(x)的极大值为g(-2)=2n-2,极小值为g(0)=0.
(Ⅱ)易知f 'n(x)=n(1+x)n-1,由 得:
得: ,
,
∴1+x0=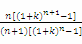 ,
,
x0=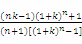 ,
,
显然(n+1)[(1+k)n-1]>0,
设h(k)=(nk-1)(1+k)n+1(k>0),
则h'(k)=n(1+k)n+n(1+k)n-1·(nk-1)=n(n+1)·k(1+k)n-1>0.
∴h(k)是(0,+∞)上的增函数,∴h(k)>h(0)=0.
故x0>0.
又x0-k=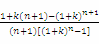 ,由(1)知,g(x)=(1+x)n-1-nx是(0,+∞)上的增函数,
,由(1)知,g(x)=(1+x)n-1-nx是(0,+∞)上的增函数,
故当x>0时,g(x)>g(0)=0,即(1+x)n>1+nx,
∴(1+k)n+1>1+(n+1)k,∴x0-k<0,x0<k.
综上所述,0<x0<k.

练习册系列答案
相关题目
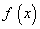 的定义域为D,如果
的定义域为D,如果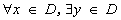 ,使得
,使得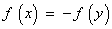 成立,则称函数
成立,则称函数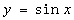 ;②
;② ;③
;③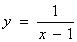 ;④
;④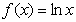 , 则其中“Ω函数”共有( )
, 则其中“Ω函数”共有( ) .其中正确命题的序号是( )
.其中正确命题的序号是( )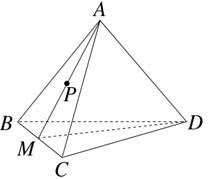
 的圆心坐标及半径分别是
的圆心坐标及半径分别是 B.
B. C.
C. D.
D.
 是等差数列,那么
是等差数列,那么 =______;
=______; 的最大值为______.
的最大值为______. ( )
( ) B.
B. C.
C.  D.
D.
 位行政领导从初一至初六值班,每天安排
位行政领导从初一至初六值班,每天安排 人,每人值班两天,则共有多少种安排方案?( )
人,每人值班两天,则共有多少种安排方案?( ) .
.
 .
.
 .
.
 .
. .
. sinAsinB=sin2C,且满足ab=4
sinAsinB=sin2C,且满足ab=4