题目内容
设P是曲线
上的动点，O为坐标原点，则OP的中点M的轨迹方程为
- A.x2+2y2=2
- B.2x2+y2=2
- C.x2+2y2=1
- D.2x2+y2=1
C
分析：设M（x，y），则P（2x，2y），代入曲线方程即可得到点M的轨迹方程．
解答：设M（x，y），则P（2x，2y），代入曲线，
得：x2+2y2=1
∴点M的轨迹方程x2+2y2=1．
故选C．
点评：本题主要考查了椭圆的简单性质、轨迹方程．代入法是圆锥曲线问题的常用方法．
分析：设M（x，y），则P（2x，2y），代入曲线方程即可得到点M的轨迹方程．
解答：设M（x，y），则P（2x，2y），代入曲线
，得：x2+2y2=1
∴点M的轨迹方程x2+2y2=1．
故选C．
点评：本题主要考查了椭圆的简单性质、轨迹方程．代入法是圆锥曲线问题的常用方法．
练习册系列答案
相关题目
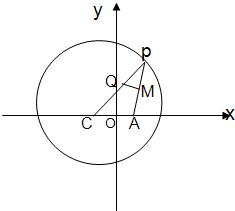已知点C为圆（x+1）2+y2=8的圆心，点A（1，0），P是圆上的动点，点Q在圆的半径CP上，且
上的一个动点，则点P到点（0，1）的距离与点P到y轴的距离之和的最小值为 ．
上的动点，O为坐标原点，则OP的中点M的轨迹方程为（ ）
上的动点，O为坐标原点，则OP的中点M的轨迹方程为（ ）