题目内容
四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
| A、3种 | B、4种 | C、5种 | D、6种 |
分析:根据题目所给条件,利用平行四边形的判定方法分别进行分析即可.
解答: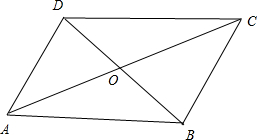 解::①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形.
解::①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形.
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形.
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形,
判定出四边形ABCD为平行四边形.
①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形,
判定出四边形ABCD为平行四边形.
故选:B.
 解::①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形.
解::①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形.③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形.
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形,
判定出四边形ABCD为平行四边形.
①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形,
判定出四边形ABCD为平行四边形.
故选:B.
点评:此题主要考查了平行四边形的判定,关键是熟练掌握平行四边形的判定定理,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
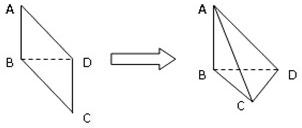
 圆内接四边形ABCD中,BA与CD的延长线交于点P,AC与BD交于点E,则图中相似三角形有( )
圆内接四边形ABCD中,BA与CD的延长线交于点P,AC与BD交于点E,则图中相似三角形有( )